BellCurveの統計解析ソフトエクセル統計

Step2. 中級編
2. 確率分布

2-1. さまざまな確率分布

ここでは、様々な確率分布やその期待値、分散について比較を行います。

■離散型確率分布

確率変数が離散型である場合の確率分布を「離散型確率分布」、あるいは「離散型分布」といいます。離散型変数はとびとびの値をとる変数のことで、隣り合う数字の間には値が存在しないものを指します。例えば、サイコロの出る目や人数などは離散型変数です。

確率分布	確率質量関数	期待値	分散
一様分布	確率変数 $X$ がとる確率がすべて等しい場合の分布 $\displaystyle P(X=k)=\frac{1}{N}$ ただし、 $k=1,2, \cdots, N$	$\displaystyle \frac {N+1}{2}$	$\displaystyle \frac {N^{2}-1}{12}$
一様分布	用語集、基礎編 15-2
ベルヌーイ分布	成功確率 $p$ の試行を行い成功回数 $X$ が成功=1もしくは失敗=0となる分布 $P(X=x)=p^x(1-p)^{1-x}$	$p$	$p(1-p)$
ベルヌーイ分布	用語集
二項分布	成功確率 $p$ のベルヌーイ試行を $n$ 回行うときの成功回数 $X$ の分布 $P(X=x)= {}_{n} \mathrm{C}_{x} p^{x} (1-p)^{n-x}$ ただし、 $x=0,1,2,\cdots,n$	$np$	$np(1-p)$
二項分布	用語集、基礎編 13-1、基礎編 13-2、中級編 3-1
超幾何分布	$M$ 個のAと $N-M$ 個のBで構成される $N$ 個からなる集団から取り出された $n$ 個の中に含まれるAの個数 $X$ の分布 $\displaystyle P(X=k)= \frac{_{M}C_{k} \times _{N-M}C_{n-k}}{_{N}C_{n}}$ ただし、 $\displaystyle \max(0,\ n - (N - M)) \leq k \leq \min(n,\ M)$	$\displaystyle n \cdot \frac{M}{N}$	$\displaystyle n \cdot \frac{M(N-M)}{N^2} \cdot \frac{N-n}{N-1}$
超幾何分布	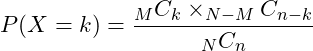用語集、基礎編 13-7
ポアソン分布	ある期間に平均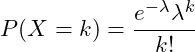 $\lambda$ 回発生する現象が起こる回数 $X$ の分布 $P(X=k)= \displaystyle\frac{e^{-\lambda} \lambda^{k}}{k!}$ ただし、 $k=0,1,2, \cdots$	$\lambda$	$\lambda$
ポアソン分布	用語集、基礎編 13-3、基礎編 13-4、基礎編 25-3、中級編 3-2
幾何分布	成功確率が $p$ の試行において、初めて成功するまでの試行回数 $X$ の分布 $P(X=k)=(1-p)^{k-1}p$ ただし、 $k=1,2,3,\cdots$	$\displaystyle \frac{1}{p}$	$\displaystyle \frac{1-p}{p^2}$
幾何分布	用語集、基礎編 13-5、基礎編 13-6、中級編 3-3
負の二項分布	成功確率が $p$ である独立なベルヌーイ試行において $k$ 回成功するまでの失敗回数 $X$ の分布 $P(X=x)=_{k+x-1}C_{x}p^{k}(1-p)^{x}$ ただし、 $k=1,2,3,\cdots$	$\displaystyle k\frac{1-p}{p}$	$\displaystyle k\frac{1-p}{p^2}$
負の二項分布	基礎編 13-8

■連続型確率分布

連続型変数は連続した値をとるものを指します。例えば、身長や体重、温度などは連続型変数です。

確率分布	確率密度関数	期待値	分散
一様分布	$a \leq X \leq b$ における一様分布は次の式で表される。 $\displaystyle f(x)= \begin{cases} \frac{1}{b-a} & a \leq X \leq b \\ 0 & X < a, X > b\end{cases}$	$\displaystyle \frac {a+b}{2}$	$\displaystyle \frac {(b-a)^2}{12}$
一様分布	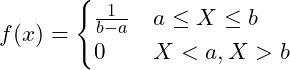用語集、基礎編 15-2
正規分布	$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}}$ ただし、 $-\infty<x<\infty$	$\mu$	$\sigma^2$
正規分布	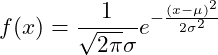用語集、基礎編 14-1、基礎編 14-2、中級編 4-1
指数分布	ある期間に平均して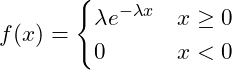 $\lambda$ 回起こる現象が、次に起こるまでの期間 $X$ が従う分布 $\displaystyle f(x) = \begin{cases} \lambda e^{- \lambda x} & x \geq 0 \\ 0 & x < 0\end{cases}$	$\displaystyle \frac{1}{ \lambda }$	$\displaystyle \frac{1}{ \lambda ^{2} }$
指数分布	用語集、基礎編 15-1
ガンマ分布	ある期間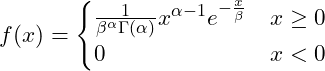 $\beta$ ごとに平均して1回起こる現象が、 $\alpha$ 回起きるまでの期間 $X$ が従う分布 $\alpha$ は形状母数、 $\beta$ は尺度母数とよばれる。 $\displaystyle f(x) =\begin{cases}{\frac{1}{\beta^\alpha\Gamma(\alpha)} x^{\alpha - 1}e^{-\frac{x}{\beta}}} & x \geq 0 \\ {0} & x < 0\end{cases}$	$\alpha \beta$	$\alpha \beta^2$
ガンマ分布	用語集
t分布	自由度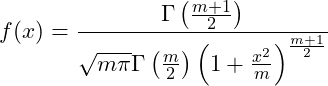 $m$ のt分布は次の式で表される。 $\Gamma()$ はガンマ関数を表す。 $\displaystyle f(x) = \frac{\Gamma \left( \frac{m+1}{2}\right)} {\sqrt{m\pi} \Gamma \left( \frac{m}{2} \right) \left( 1+ \frac{x^2}{m} \right)^{\frac{m+1}{2}}} \hspace{20px}$ ただし、 $-\infty<x<\infty$	$0$ $(m>1)$	$\displaystyle \frac{m}{m-2}$ $(m>2)$
t分布	用語集、基礎編 20-1、基礎編 20-2
カイ二乗分布	正規分布に従ういくつかの変数の二乗和が従う分布自由度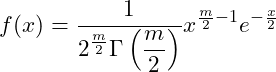 $m$ のカイ二乗分布は次の式で表される。 $\Gamma()$ はガンマ関数を表す。 $\displaystyle f(x) = \frac{1}{2^{\frac{m}{2}}\displaystyle \Gamma \left(\frac{m}{2}\right)} x^{\frac{m}{2}-1}e^{-\frac{x}{2}} \hspace{20px}$ ただし、 $0 \leq x < \infty$	$n$	$2n$
カイ二乗分布	用語集、基礎編 22-1、基礎編 22-2
F分布	カイ二乗分布に従う2変数の比が従う分布自由度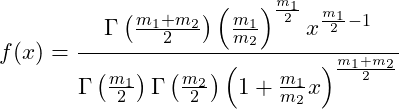 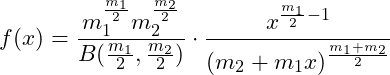$(m_1, m_2)$ のF分布は次の式で表される。 $\Gamma()$ はガンマ関数を、 $B()$ はベータ関数を表す。 $\displaystyle f(x) = \frac{\Gamma \left( \frac{m_1 + m_2}{2}\right) \left(\frac{m_1}{m_2}\right) ^{\frac{m_1}{2}} x^{\frac{m_1}{2} - 1}} {\Gamma \left( \frac{m_1}{2} \right) \Gamma \left( \frac{m_2}{2} \right) \left( 1 + \frac{m_1}{m_2}x \right)^{\frac{m_1 + m_2}{2}}} \hspace{20px}$ あるいは $\displaystyle f(x) = \frac{m_1^{\frac{m_1}{2}}m_2^{\frac{m_2}{2}}}{B(\frac{m_1}{2}, \frac{m_2}{2})} \cdot \frac{x^{\frac{m_1}{2}-1}}{(m_2+m_1x)^{\frac{m_1+m_2}{2}}}$	$\displaystyle \frac{m_2}{m_2-2}$ $(m_2>2)$	$\displaystyle \frac{2{n_2}^2(m_1 +m_2-2)}{m_1(m_2-2)^2(m_2-4)}$ $(m>4)$
F分布	用語集、基礎編 28-1、基礎編 28-2

2. 確率分布

統計学やデータ分析を学ぶなら、大人のための統計教室和（なごみ）［業務提携］

90分で学ぶ　大人のための「統計超入門」

chatGPTで学ぶ「統計学」　はじめての方向け爆速習得講座

【BellCurve監修】統計検定^®2級対策に最適な模擬問題集1～3を各500円（税込）にて販売中！

Kindleストアで配信中

統計検定^®2級模擬問題集1

500円（税込）

統計検定^®2級模擬問題集2

500円（税込）

統計検定^®2級模擬問題集3

500円（税込）