- Step1. 基礎編
- 13. いろいろな確率分布1
13-6. 幾何分布の期待値と分散
確率変数![]() が成功確率
が成功確率![]() の幾何分布に従っている時、その期待値
の幾何分布に従っている時、その期待値![]() と分散
と分散![]() は以下のようになります。
は以下のようになります。
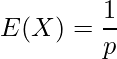
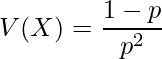
例えば、さいころを投げて1が出る確率![]() であることから、初めて1が出るまでの回数の期待値は次のように6回と計算できます。
であることから、初めて1が出るまでの回数の期待値は次のように6回と計算できます。
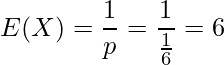
例題:
A、Bの2人でじゃんけんをするとき、5回目で勝敗が決まる確率はいくらでしょうか。また、勝敗が決まるまでのじゃんけんの回数の期待値はいくらでしょうか。
| A | B | 勝敗 |
|---|---|---|
| グー | グー | あいこ |
| グー | チョキ | A勝ち |
| グー | パー | B勝ち |
| チョキ | グー | B勝ち |
| チョキ | チョキ | あいこ |
| チョキ | パー | A勝ち |
| パー | グー | A勝ち |
| パー | チョキ | B勝ち |
| パー | パー | あいこ |
A、Bの2人でじゃんけんを1回行う場合、Aが勝つ確率は![]() 、Bが勝つ確率も同様に
、Bが勝つ確率も同様に![]() 、あいこになる確率は
、あいこになる確率は![]() です。したがって、勝敗が決まる確率は
です。したがって、勝敗が決まる確率は![]() です。5回目で勝敗が決まる確率は次のように計算できます。
です。5回目で勝敗が決まる確率は次のように計算できます。
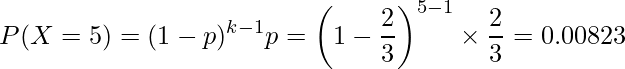
また、勝敗が決まるまでの回数の期待値は、次の式から1.5回と計算できます。
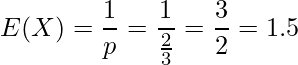
【コラム】幾何分布の無記憶性
幾何分布には「無記憶性」という性質があります。これは、「ある事象が発生する確率は、その事象が発生する前の情報の影響を受けない」というものです。例えば、「コインを投げて3回目ではじめて表が出る確率を考える場合に、1回目、2回目に連続で裏が出たとしても、3回目に表が出る確率はそれまでと同じで変化することない(=表が出る確率が高くなるといったことはない)、というのが無記憶性です。つまり、![]() 回目で表が出る確率は過去の影響を受けること無く、独立した結果となります。
回目で表が出る確率は過去の影響を受けること無く、独立した結果となります。
13. いろいろな確率分布1
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 13. いろいろな確率分布1
13-5. 幾何分布
- ブログ
確率変数とは







