13-5. 幾何分布

■幾何分布

成功確率が $p$ である独立なベルヌーイ試行を繰り返す時、初めて成功するまでの試行回数 $X$ が従う確率分布を「幾何分布（きかぶんぷ）」といいます。確率変数 $X$ が幾何分布に従う場合、成功確率が $p$ の試行において、 $k$ 回目で初めて成功する確率（ $X=k$ となる確率）は次の式から計算できます。

$\begin{eqnarray*} P(X=k)=(1-p)^{k-1} p & (k=1,2,3,\cdots) \\ \end{eqnarray*}$

例えば、さいころを投げて1が出る確率は $p= \displaystyle\frac{1}{6}$ であることから、3投目で初めて1が出る確率は次のように約11.6%と計算できます。

$\displaystyle P(X=3)=(1-p)^{k-1} p=\left(1-\frac{1}{6}\right)^{3-1} \times \frac{1}{6}=0.116$

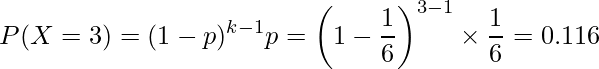
■幾何分布のグラフ

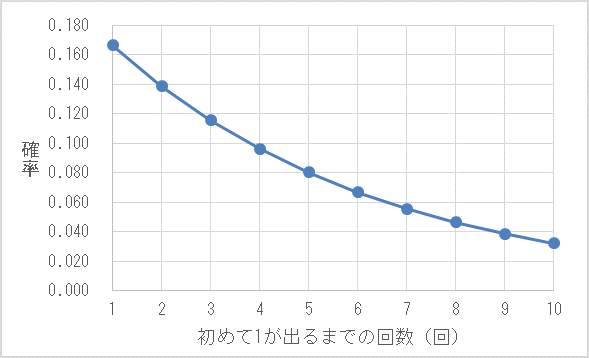
同様の計算を行い、さいころを投げて初めて1が出るまでの回数の確率を表にまとめました。

初めて1が出るまでに投げる回数	確率
1	0.167
2	0.139
3	0.116
4	0.096
5	0.080
6	0.067
7	0.056
8	0.047
9	0.039
10	0.032

この表から幾何分布のグラフを描くと次のようになります。さいころを投げて初めて1が出るまでの回数が1回となる時の確率が最も高く、その回数が多くなるにつれて確率はなだらかに低くなっていることが分かります。

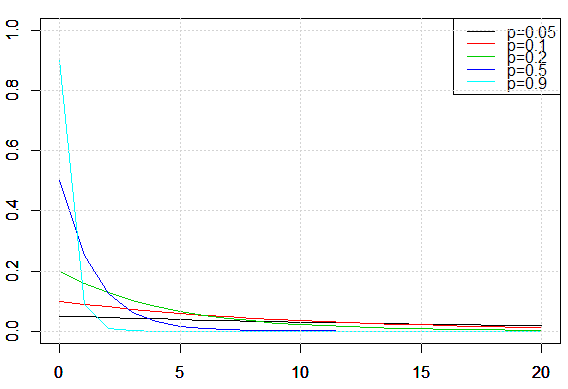
さまざまな幾何分布の形を見てみます。成功確率 $p$ を変化させたとき、その大小でグラフがどのように変化するかを表したものが次の図です。このグラフでは成功確率 $p$ を0.05、0.1、0.2、0.5、0.9にしています。横軸は試行回数 $k+1$ 、縦軸は成功確率 $p$ を表します。 $p$ が大きくなるほどグラフの傾きは急になることが分かります。