- Step1. 基礎編
- 13. いろいろな確率分布1
13-7. 超幾何分布
■超幾何分布
AとBで構成される![]() 個からなる集団があり、Aが
個からなる集団があり、Aが![]() 個、Bが
個、Bが![]() 個であるとします。この集団から取り出された
個であるとします。この集団から取り出された![]() 個の中に含まれるAの個数が従う確率分布を「超幾何分布(ちょうきかぶんぷ)」といいます。確率変数が超幾何分布に従う場合、取り出されたAが
個の中に含まれるAの個数が従う確率分布を「超幾何分布(ちょうきかぶんぷ)」といいます。確率変数が超幾何分布に従う場合、取り出されたAが![]() 個である確率(
個である確率(![]() となる確率)は次の式から計算できます。
となる確率)は次の式から計算できます。
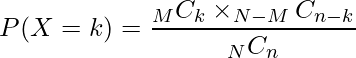
ただし、![]() は次の条件を満たします。
は次の条件を満たします。
例えば、赤い玉が8個と白い玉が5個入った袋から3つの玉を取り出したときに、3つのうち2つが赤色の玉である確率は次のように計算できます。
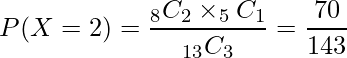
■例題1:
ある湖に魚が100匹います。このうち、20匹の魚を捕獲して尾びれに印をつけて湖に戻しました。この湖から5匹の魚を捕獲したとき、尾びれに印がついた魚が1匹だけ含まれる確率はいくらでしょうか。

全体の魚の数は![]() 、印がついた魚の数は
、印がついた魚の数は![]() 、印がついていない魚の数は
、印がついていない魚の数は![]() 、捕獲した魚の数は
、捕獲した魚の数は![]() であることから、
であることから、
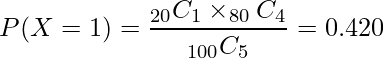
と計算され、尾びれに印がついた魚が1匹だけ含まれる確率は約42.0%となります。
■例題2:
ある湖にいる魚を100匹捕獲して尾びれに印をつけて湖に戻しました。この湖から20匹の魚を捕獲したとき、尾びれに印がついた魚が5匹含まれていました。このとき、湖全体には何匹の魚がいると推定できるでしょうか。

捕獲した20匹の魚のうち、印がついた魚は5匹でした。つまり、ランダムに捕獲した魚の5/20=1/4には印がついていることが予想されます。湖全体の魚についても同様の割合で印がついていることが予想されることから、湖全体の魚の数を![]() とすると
とすると
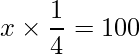
という式を立てることができます。これを解いて![]() となり、湖には400匹の魚がいると推定できます。
となり、湖には400匹の魚がいると推定できます。
このように、一部の個体を捕獲して印をつけ、再度捕獲したときの印の数をもとに全体の個体数を推定する方法を「捕獲再捕獲法」といいます。ある領域や地域に住む生物の個体数を推定するときに使われます。ただし、ほとんど移動しない生物や個体数が変化する生物に対して個体数の推定を行う場合には、捕獲再捕獲法は適していません。
■超幾何分布の期待値と分散
確率変数![]() が超幾何分布に従っている時、その期待値
が超幾何分布に従っている時、その期待値![]() と分散
と分散![]() は以下のようになります。
は以下のようになります。
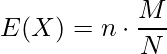
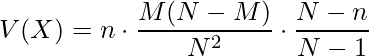
超幾何分布は、2つの性質で構成される集団から非復元抽出法でサンプルを採取した場合の確率分布です。復元抽出法の場合には![]() (一定)とおくことができます。このとき、期待値と分散は
(一定)とおくことができます。このとき、期待値と分散は
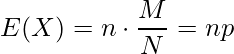
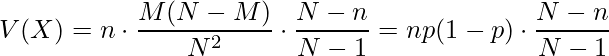
となります。![]() が無限に大きい場合(
が無限に大きい場合(![]() )には
)には
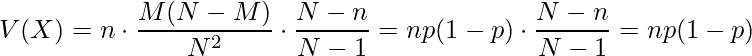
となり、二項分布における期待値と分散に等しくなります。つまり、![]() (一定)であり
(一定)であり![]() が無限に大きい場合(
が無限に大きい場合(![]() )には、超幾何分布は二項分布に近似できます。
)には、超幾何分布は二項分布に近似できます。






