- Step1. 基礎編
- 13. いろいろな確率分布1
13-1. 二項分布
■ベルヌーイ試行
「コインを投げたときに表が出るか裏が出るか」のように、何かを行ったときに起こる結果が2つしかない試行のことを「ベルヌーイ試行」といいます。ベルヌーイ試行では一般に、2つの結果のうち一方を「成功」とし、確率変数![]() がとる値を「1」、もう一方の結果を「失敗」とし、確率変数
がとる値を「1」、もう一方の結果を「失敗」とし、確率変数![]() がとる値を「0」とします。そして成功の確率を
がとる値を「0」とします。そして成功の確率を![]() とすると、それぞれの確率は次のように表されます。
とすると、それぞれの確率は次のように表されます。
■二項分布
このベルヌーイ試行を![]() 回行って、成功する回数
回行って、成功する回数![]() が従う確率分布を「二項分布」といいます。また、
が従う確率分布を「二項分布」といいます。また、![]() が二項分布に従うとき、「
が二項分布に従うとき、「![]() 」と書きます。
」と書きます。![]() や
や![]() は確率分布を特徴づける値であり、「パラメータ(母数)」と呼ばれます(分母や母集団の大きさのことを母数というのは誤りです)。
は確率分布を特徴づける値であり、「パラメータ(母数)」と呼ばれます(分母や母集団の大きさのことを母数というのは誤りです)。
![]() 回のベルヌーイ試行を行うときにちょうど
回のベルヌーイ試行を行うときにちょうど![]() 回成功する確率、すなわち
回成功する確率、すなわち![]() となる確率は次の式から計算することができます。
となる確率は次の式から計算することができます。
![]()
例えば、コインを10回投げて表が3回出る確率は、表が出る確率が![]() であることから、次のように計算できます。
であることから、次のように計算できます。
■二項分布のグラフ
同様の計算を行い、コインを10回投げて表が出る回数の確率を表にまとめました。
| 表の出る回数 | 確率 |
|---|---|
| 0 | 0.001 |
| 1 | 0.010 |
| 2 | 0.044 |
| 3 | 0.117 |
| 4 | 0.205 |
| 5 | 0.246 |
| 6 | 0.205 |
| 7 | 0.117 |
| 8 | 0.044 |
| 9 | 0.010 |
| 10 | 0.001 |
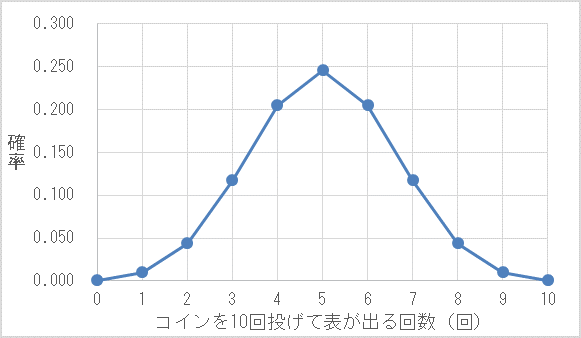
この表から二項分布のグラフを描くと次のようになります。表の出る回数が5回となる時の確率が最も高く、表の出る回数が5回より多く、もしくは少なくなるにつれて、確率は低くなっていることが分かります。
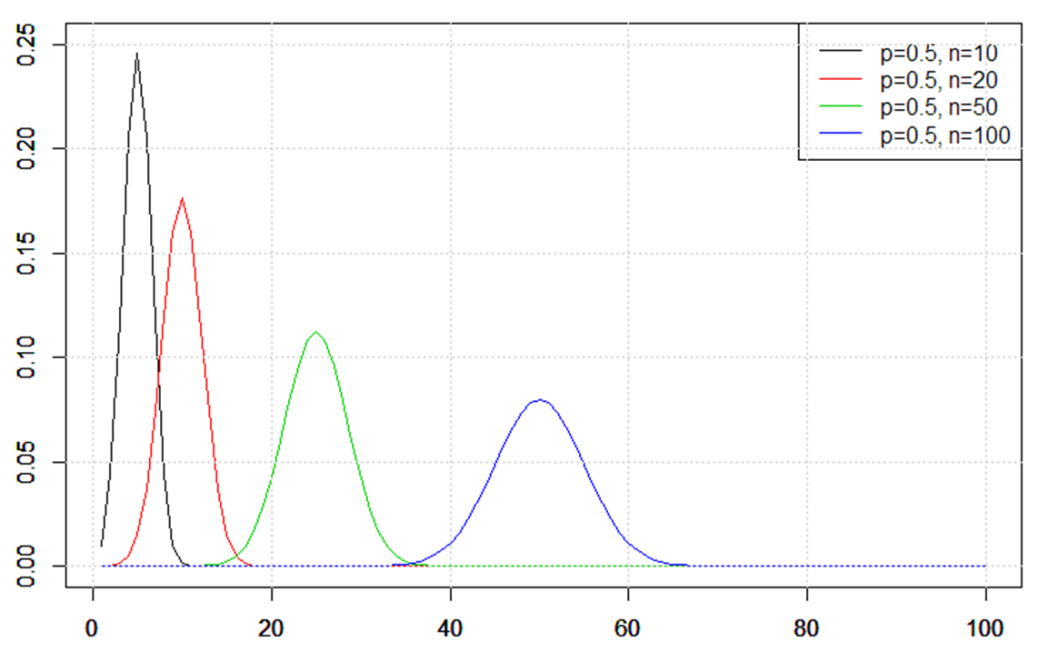
次に、さまざまな二項分布のグラフの形を見てみます。前述の例はコインを10回投げて表が出る回数![]() の確率を表したものでしたが、コインを投げる回数(=試行回数)
の確率を表したものでしたが、コインを投げる回数(=試行回数)![]() を20、50、100回と増やした場合、コインの表が出る回数
を20、50、100回と増やした場合、コインの表が出る回数![]() の確率のグラフは次のようになります。横軸は成功回数
の確率のグラフは次のようになります。横軸は成功回数![]() を、縦軸はそのときの確率
を、縦軸はそのときの確率![]() を表しています。
を表しています。
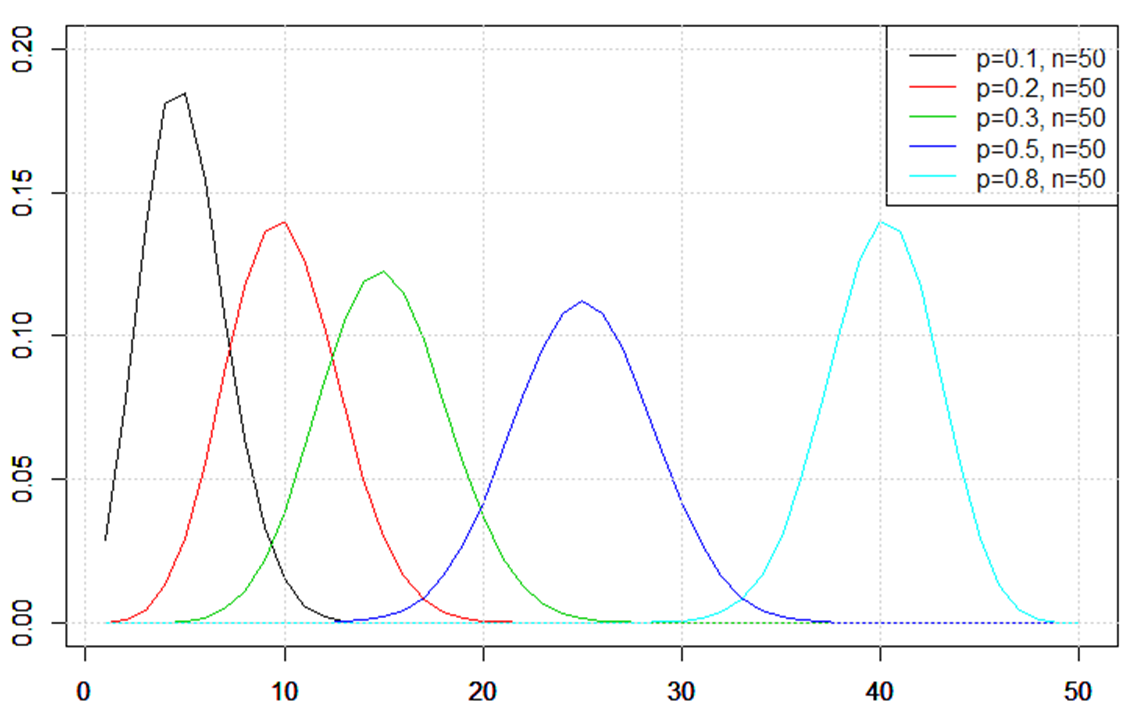
また、試行回数を固定し成功確率![]() を変化させたときに、
を変化させたときに、![]() の大小でグラフがどのように変化するかを表したものが次の図です。このグラフでは試行回数
の大小でグラフがどのように変化するかを表したものが次の図です。このグラフでは試行回数![]() を50回に固定し、成功確率
を50回に固定し、成功確率![]() を0.1、0.2、0.3、0.5、0.8にしています。試行回数
を0.1、0.2、0.3、0.5、0.8にしています。試行回数![]() が大きくなるほど、同様に成功確率
が大きくなるほど、同様に成功確率![]() が大きくなるほどグラフの山は右側へスライドしていることが分かります。
が大きくなるほどグラフの山は右側へスライドしていることが分かります。
■おすすめ書籍
ゆる~いかんじですが、二項分布の説明は手厚いです。
13. いろいろな確率分布1
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 9. 確率と期待値
9-1. 確率
- 11. 確率変数と確率分布
11-2. 離散型確率分布と確率質量関数
- 11. 確率変数と確率分布
11-3. 連続型確率分布
- ブログ
確率変数とは
- ブログ
二項検定







