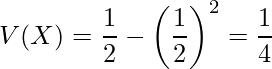- 12. 累積分布関数と確率変数の期待値・分散
練習問題(12. 累積分布関数と確率変数の期待値・分散)
1
1から100までの数字が書いてある100枚のカードの中からランダムに1枚引く。このとき、引いたカードに書いてある数字を確率変数![]() とすると、1から100までの
とすると、1から100までの![]() について確率分布
について確率分布![]() を考えることができる。
を考えることができる。
この確率分布![]() の累積分布関数
の累積分布関数![]() について、次の4つの数値がそれぞれどのような事象を表すか答えよ。
について、次の4つの数値がそれぞれどのような事象を表すか答えよ。

答えを見る
- 答え
 閉じる
閉じる -
- 5以下のカードを引く確率
- 90以下のカードを引く確率
- 40~50のカードを引く確率
- 20~30または75~80のカードを引く確率
2
3枚の異なるコインを投げるとき、表が出る枚数を確率変数![]() とする。このとき、確率変数
とする。このとき、確率変数![]() の期待値と分散を求めよ。
の期待値と分散を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
確率変数
 がとり得るそれぞれの値に対応する確率
がとり得るそれぞれの値に対応する確率 をまとめると次のようになります。
をまとめると次のようになります。表が出る枚数 (  )
)0 1 2 3 確率 ( 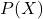 )
)



したがって、期待値は次のように計算できます。
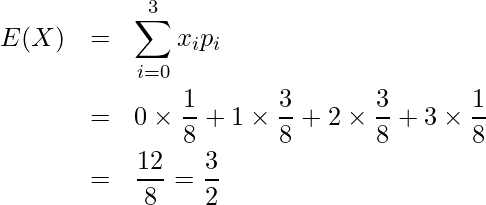
分散は期待値を用いて次の式から求められます。
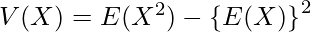
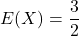 を使って、まず
を使って、まず を求めます。
を求めます。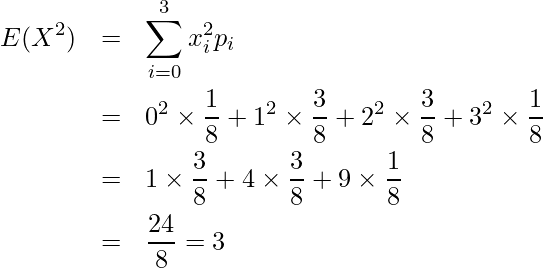
次に
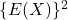 を求めます。
を求めます。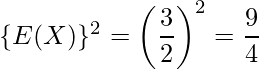
したがって次のように計算できます。
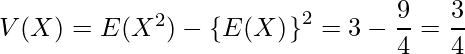
3
次のような確率密度関数があるとき、確率変数![]() の期待値と分散を求めよ。
の期待値と分散を求めよ。
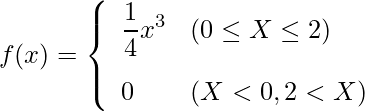

答えを見る
- 答え
 閉じる
閉じる -
期待値は次のように計算できます。
![Rendered by QuickLaTeX.com \begin{eqnarray*} E(X)&=& \displaystyle \int_{0}^{2} xf(x)dx \\ &=&\displaystyle \int_{0}^{2} x \times \displaystyle \frac{1}{4}x^3 dx \\ &=&\displaystyle \int_{0}^{2} \displaystyle \frac{1}{4}x^4 dx \\ &=&\left[ \displaystyle \frac{x^5}{20} \right]_0^2 \\ &=&\displaystyle \frac{32}{20} = \displaystyle \frac{8}{5} \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-7bf3f1bdc8990f75ed8be48e34dae9d4_l3.png)
分散は期待値を用いて次の式から求められます。
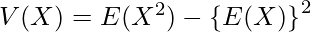
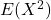 は次のように求めます。
は次のように求めます。![Rendered by QuickLaTeX.com \begin{eqnarray*} E(X^2)&=& \displaystyle \int_{0}^{2} x^2f(x)dx \\ &=&\displaystyle \int_{0}^{2} x^2 \times \displaystyle \frac{1}{4}x^3 dx \\ &=&\displaystyle \int_{0}^{2} \displaystyle \frac{1}{4}x^5 dx \\ &=&\left[ \displaystyle \frac{x^6}{24} \right]_0^2 \\ &=&\displaystyle \frac{64}{24} = \displaystyle \frac{8}{3} \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-b3349d0ea5233886410865a8585357d3_l3.png)
次に
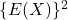 を求めます。
を求めます。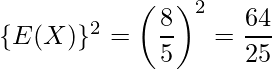
したがって次のように計算できます。
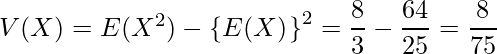
4
1枚のコインを投げるとき、確率変数![]() を裏が出たら
を裏が出たら![]() 、表が出たら
、表が出たら![]() と対応させる。この確率変数
と対応させる。この確率変数![]() が従う確率分布について、累積分布関数
が従う確率分布について、累積分布関数![]() を求めよ。
を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
 は0と1しか値をとらず、どちらの場合においても
は0と1しか値をとらず、どちらの場合においても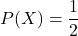 です。
累積分布関数の定義に従って、次のように
です。
累積分布関数の定義に従って、次のように を求めることができます。
を求めることができます。
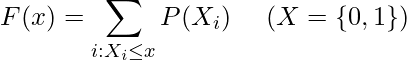
 について
について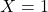 について
について
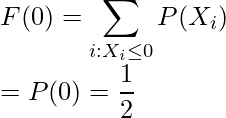
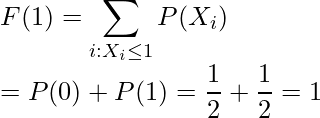
以上の事から、累積分布関数は次のようになります。
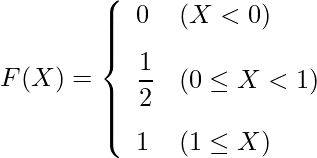
これをグラフにすると次のようになります。
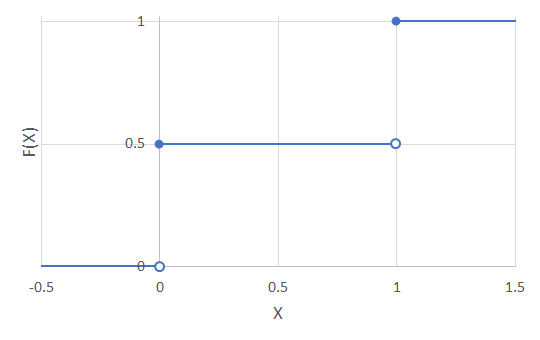
5
1枚のコインを投げるとき、確率変数![]() を裏が出たら
を裏が出たら![]() 、表が出たら
、表が出たら![]() と対応させる。
この確率変数
と対応させる。
この確率変数![]() が従う確率分布について、分散
が従う確率分布について、分散![]() を求めよ。
を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
 は0と1しか値をとらず、どちらの場合においても
は0と1しか値をとらず、どちらの場合においても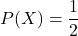 です。離散型確率分布における分散は次のように求めます。
です。離散型確率分布における分散は次のように求めます。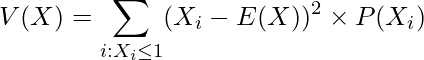
難しく見えますが、
 は0か1の二つしかなく
は0か1の二つしかなく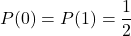 であるので、次のようになります。
であるので、次のようになります。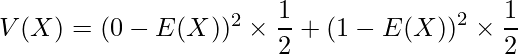
期待値
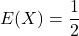 を用いると、分散
を用いると、分散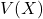 は
は と計算できます。
と計算できます。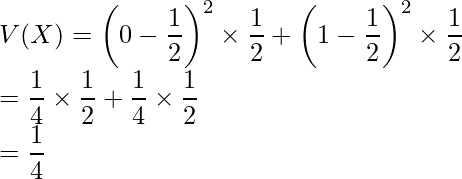
分散のもう1つの計算式
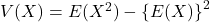 を用いて分散を計算することもできます。まず、
を用いて分散を計算することもできます。まず、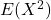 を求めます。
を求めます。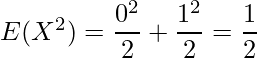
これを用いて、
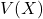 を計算します。
を計算します。