- Step1. 基礎編
- 12. 累積分布関数と確率変数の期待値・分散
12-2. 累積分布関数の性質
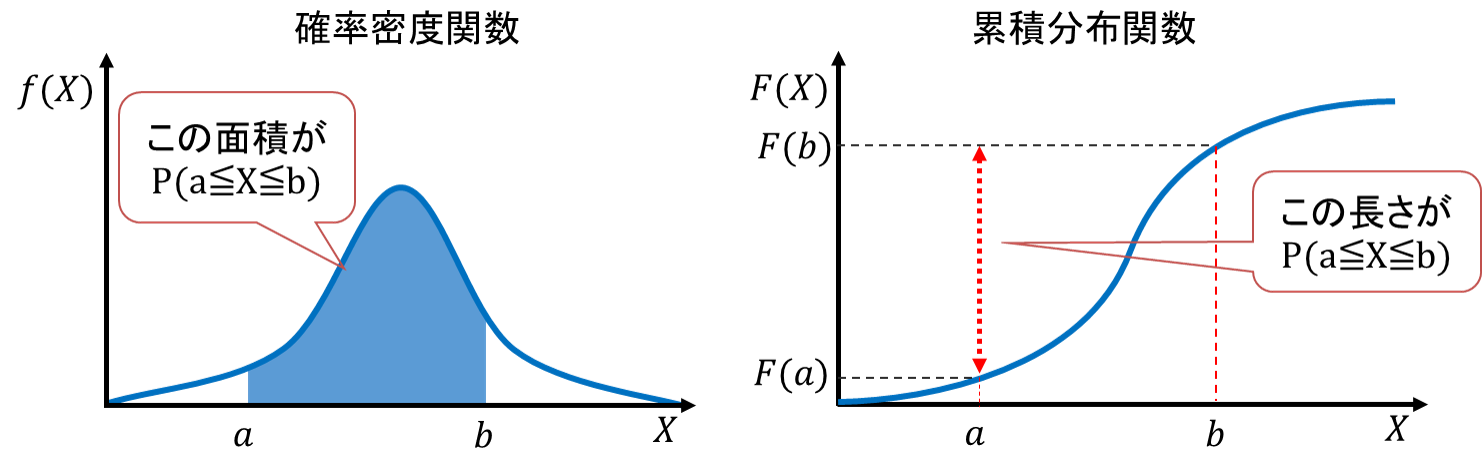
累積分布関数では、確率変数がとる値が離散型、連続型のいずれにおいても以下の事項が成り立ちます。
1. F(∞)=1
この式は確率変数![]() がとる値が無限大以下となる確率は1であることを示しています。11-5章で学んだように、確率変数がとるすべての値の和である
がとる値が無限大以下となる確率は1であることを示しています。11-5章で学んだように、確率変数がとるすべての値の和である![]() は1に等しくなるためです。
は1に等しくなるためです。
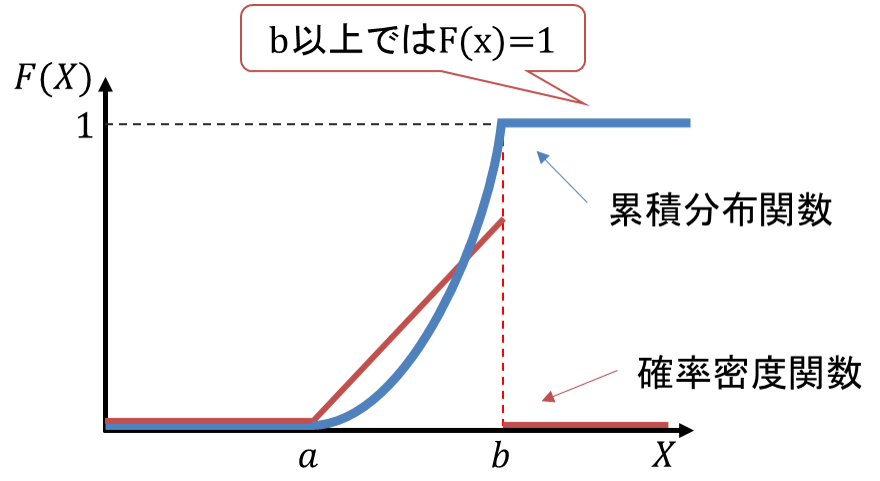
確率変数がある範囲の値しかとらないときには、![]() がとる値がその範囲の最大値以上となる場合においてこの式が成立します。例えば確率変数
がとる値がその範囲の最大値以上となる場合においてこの式が成立します。例えば確率変数![]() がとる値が
がとる値が![]() 以上
以上![]() 以下である場合
以下である場合![]() 、
、![]() 以上では累積分布関数
以上では累積分布関数![]() となります。
となります。
2. F(-∞)=0
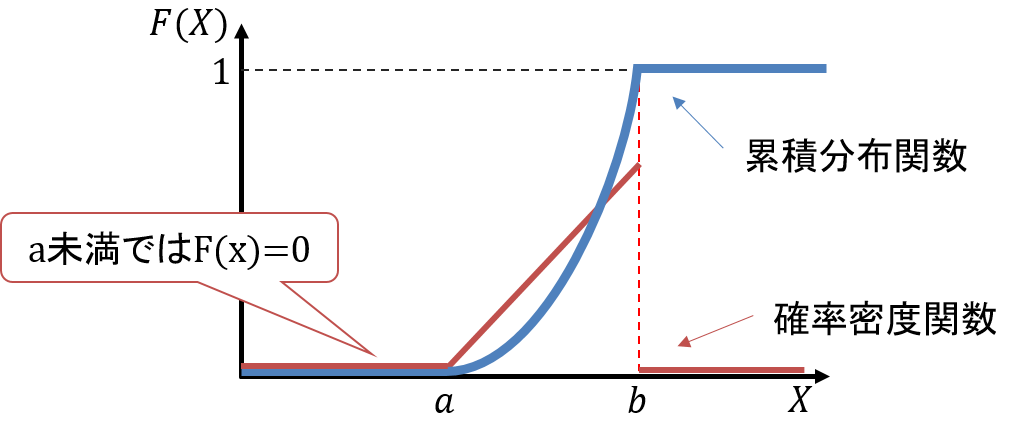
この式は確率変数![]() がとる値がマイナス無限大となる確率は0であることを示しています。確率変数がある範囲の値しかとらないときには、
がとる値がマイナス無限大となる確率は0であることを示しています。確率変数がある範囲の値しかとらないときには、![]() がとる値がその範囲の最小値以下となる場合においてこの式が成立します。例えば確率変数がとる値が
がとる値がその範囲の最小値以下となる場合においてこの式が成立します。例えば確率変数がとる値が![]() 以上
以上![]() 以下である場合
以下である場合![]() 、
、![]() 未満の
未満の![]() において累積分布関数
において累積分布関数![]() となります。
となります。
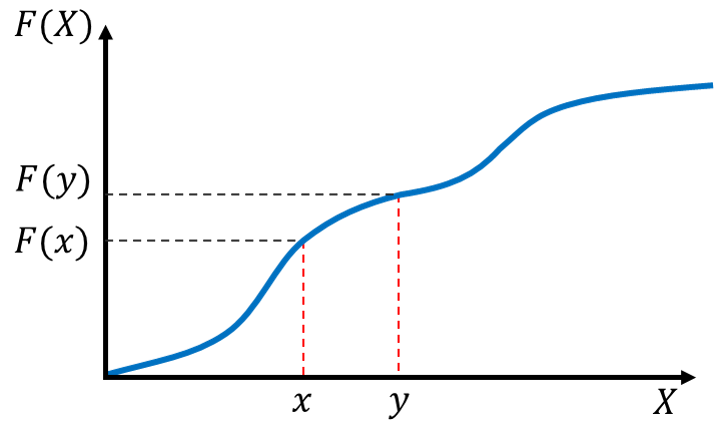
3. X≦Yである場合F(X)≦F(Y)
この式は確率変数![]() がとる値よりも
がとる値よりも![]() がとる値の方が大きい場合、その累積分布関数
がとる値の方が大きい場合、その累積分布関数![]() よりも
よりも![]() の方が大きくなることを示しています。確率質量関数および確率密度関数では常に
の方が大きくなることを示しています。確率質量関数および確率密度関数では常に![]() が成立するため、和を取った(あるいは積分した)ものである累積分布関数は、
が成立するため、和を取った(あるいは積分した)ものである累積分布関数は、![]() が大きくなるにつれ
が大きくなるにつれ![]() の値も必ず増加します(減少することは絶対にありません)。
の値も必ず増加します(減少することは絶対にありません)。
【コラム】累積分布関数と確率
「確率変数![]() がとる値が
がとる値が![]() となる確率」は確率質量関数もしくは確率密度関数から求められます。
となる確率」は確率質量関数もしくは確率密度関数から求められます。
- 離散型確率変数の場合
- 連続型確率変数の場合
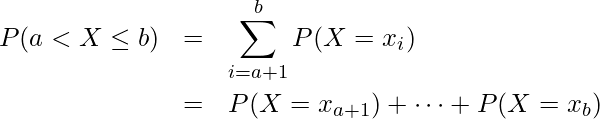
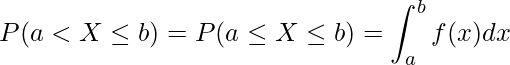
「確率変数![]() がとる値が
がとる値が![]() となる確率」は累積分布関数を用いても算出できます。この場合、次の式を用います。
となる確率」は累積分布関数を用いても算出できます。この場合、次の式を用います。
- 離散型確率変数の場合
- 連続型確率変数の場合
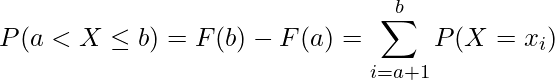
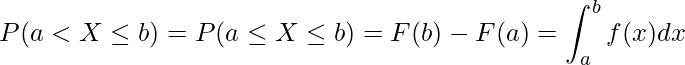
12. 累積分布関数と確率変数の期待値・分散
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 12. 累積分布関数と確率変数の期待値・分散
12-1. 累積分布関数とは







