- Step1. 基礎編
- 12. 累積分布関数と確率変数の期待値・分散
12-5. 確率変数の分散
分散は、「確率変数のとり得る値と期待値(平均値)の差の2乗」と「確率」との積を、全て足し合わせたものです。分散はVarianceの頭文字の「![]() 」を用いて表します。例えば、確率変数
」を用いて表します。例えば、確率変数![]() についての分散は「
についての分散は「![]() 」と表します。
」と表します。
分散を計算することで、確率変数![]() のとる値が期待値の周りにどの程度ばらついているかが分かります。分散が小さいほど確率変数の取りうる値は期待値に集まっていることを表します。6-2章で学んだように、分散の単位は元の単位の2乗であることに注意してください。
のとる値が期待値の周りにどの程度ばらついているかが分かります。分散が小さいほど確率変数の取りうる値は期待値に集まっていることを表します。6-2章で学んだように、分散の単位は元の単位の2乗であることに注意してください。
■離散型確率変数の場合
離散型確率変数![]() の分散は次の式で計算できます。ただし、
の分散は次の式で計算できます。ただし、![]() の期待値を
の期待値を![]() (ミュー)とします。
(ミュー)とします。
| ・・・ | |||||
| ・・・ |
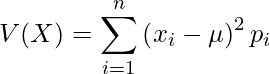
例えばさいころを投げて出る目を確率変数![]() とするとき、分散は次のように計算できます。ただし、
とするとき、分散は次のように計算できます。ただし、![]() であることを用います。
であることを用います。
| さいころの出る目 ( | 1 | 2 | 3 | 4 | 5 | 6 |
| 確率 ( |
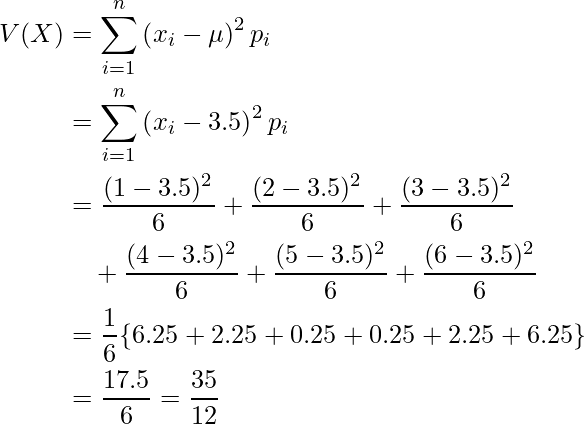
■連続型確率変数の場合
連続型確率変数![]() の分散は、次の式で計算できます。ただし、確率変数の期待値を
の分散は、次の式で計算できます。ただし、確率変数の期待値を![]() とします。
とします。
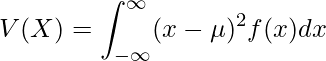
例えば確率密度関数![]() において、確率変数
において、確率変数![]() が0から6の範囲をとるとき
が0から6の範囲をとるとき![]() 、分散は次のようになります。ただし、
、分散は次のようになります。ただし、![]() であることを用います。
であることを用います。
![Rendered by QuickLaTeX.com \begin{eqnarray*} V(X)&=& \displaystyle \int_{-\infty}^{\infty} (x-\mu )^2 f(x)dx \\ &=&\displaystyle \int_{0}^{6} (x-3 )^2 \times \displaystyle \frac{1}{6}dx \\ &=& \left[ \displaystyle \frac{(x-3)^3}{18} \right]_0^6 \\ &=&\displaystyle \frac{27}{18}- \left\{ -\frac{27}{18}\right\} \\ &=& 3 \\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-7b17e9b8a1364555161467fe4f0a32b8_l3.png)
【コラム】分散を期待値から求める
分散は期待値を用いて次の式から求められます。
この等式は、分散の式を変形することで得られます。
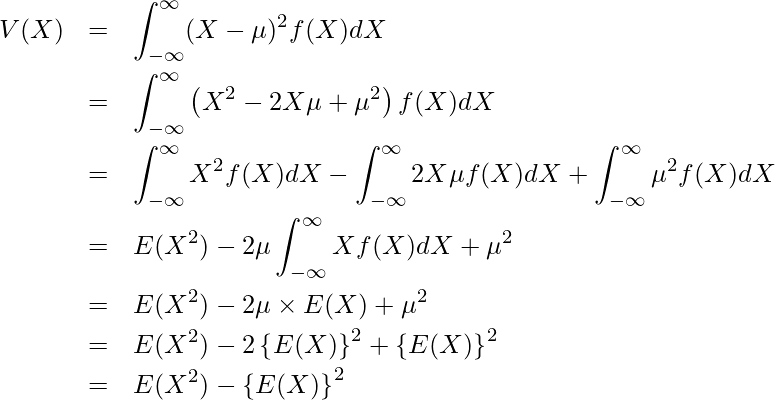
最後は、![]() の関係を用いています。さいころを投げるときの出る目を
の関係を用いています。さいころを投げるときの出る目を![]() とするとき、
とするとき、![]() 、
、![]() と計算されました。この分散の値を期待値から求める場合、
と計算されました。この分散の値を期待値から求める場合、
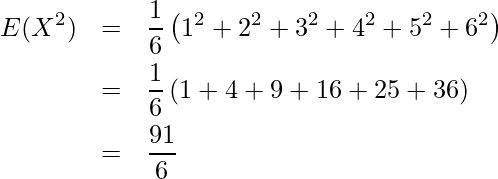
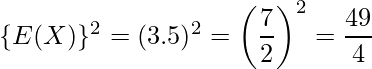
となることから次のように計算できます。
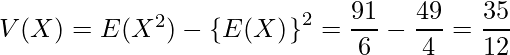
| さいころの出る目 ( | 1 | 2 | 3 | 4 | 5 | 6 |
| (さいころの出る目) | 1 | 4 | 9 | 16 | 25 | 36 |
| 確率 ( |
12. 累積分布関数と確率変数の期待値・分散
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 6. 分散と標準偏差
6-1. 分散
- 6. 分散と標準偏差
6-2. 標準偏差
- 12. 累積分布関数と確率変数の期待値・分散
12-3. 確率変数の期待値







