- Step1. 基礎編
- 6. 分散と標準偏差
6-2. 標準偏差
分散は「データがどの程度平均値の周りにばらついているか」を表す指標です。ただし、注意しなければならないのは「分散同士は比べることはできるが、分散と平均を足し算したり、分散と平均を比較したりすることはできない」という点です。これは、分散を計算する際に各データを2乗したものを用いていることが原因です。
例えば100人の身長を「cm」の単位で測定した場合には、平均の単位は「cm」となりますが、分散の単位はその2乗の「cm2」となるため、平均と分散の値をそのまま比較したり計算したりすることはできません。
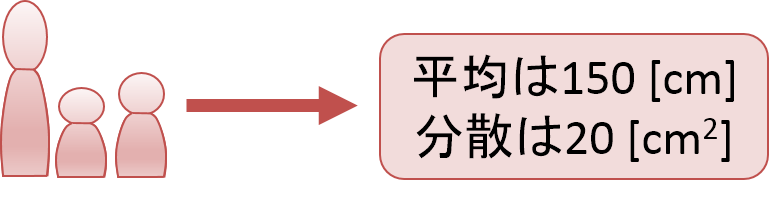
そこで、分散の「平方根」を計算することで2乗された単位は元に戻り、足したり引いたりすることができるようになります。分散の正の平方根のことを「標準偏差」と言います。
![]()
英語では、standard deviationと表記され、SDと略されることもあります。記号は「![]() (小文字のシグマ)」を用いて表されることが多く、分散の正の平方根であることから分散を「
(小文字のシグマ)」を用いて表されることが多く、分散の正の平方根であることから分散を「![]() 」と表すこともあります。標準偏差は分散と同様に、「データがどの程度ばらついているか」の指標であり、値が大きいほどばらつきが大きいことを示します。
」と表すこともあります。標準偏差は分散と同様に、「データがどの程度ばらついているか」の指標であり、値が大きいほどばらつきが大きいことを示します。
6‐1章のデータAとデータBから標準偏差を求めてみます。
| データA | 平均値からの差 | (平均値からの差)2 |
|---|---|---|
| 1 | 2.5 | 6.25 |
| 2 | 1.5 | 2.25 |
| 3 | 0.5 | 0.25 |
| 4 | -0.5 | 0.25 |
| 5 | -1.5 | 2.25 |
| 6 | -2.5 | 6.25 |
| 合計=21 | 合計=0 | 合計=17.5 |
| 平均=3.5 | - | 分散=17.5/6≒2.9 |
| - | - | 標準偏差=√2.9≒1.7 |
| データB | 平均値からの差 | (平均値からの差)2 |
|---|---|---|
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 3.5 | 0 | 0 |
| 合計=21 | 合計=0 | 合計=0 |
| 平均=3.5 | - | 分散=0/6≒0 |
| - | - | 標準偏差=√0≒0 |
この結果から、データAとデータBの標準偏差は次のようになります。
- データAの標準偏差:
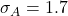 あるいは
あるいは 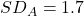
- データBの標準偏差:
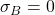 あるいは
あるいは 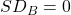
標準偏差は分散と同様にデータAの方が大きいことから、データAの方がデータBよりもばらついていることが分かります。
6. 分散と標準偏差
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計解析事例
記述統計量
- 1. 統計ことはじめ
1-1. ギリシャ文字の読み方
- 6. 分散と標準偏差
6-1. 分散
- ブログ
STDEVとSTDEVP







