- 6. 分散と標準偏差
練習問題(6. 分散と標準偏差)
1
次のデータについて、偏差および偏差の合計を求めよ。
データ:13 6 5 12 9

答えを見る
- 答え
 閉じる
閉じる -
偏差は各データから平均を引いた値です。偏差の合計は次の表に示すように0になります。
No. データ 偏差 1 13 4 2 6 -3 3 5 -4 4 12 3 5 9 0 合計 45 0 平均 9 -
2
次のデータについて、平均偏差を求めよ。
データ:13 6 5 12 9

答えを見る
- 答え
 閉じる
閉じる -
平均偏差は偏差の絶対値の平均値です。この値は次の表に示すように2.8になります。
No. データ 偏差の絶対値 1 13 4 2 6 3 3 5 4 4 12 3 5 9 0 合計 45 14 平均 9 2.8(=平均偏差)
3
次のデータについて、分散および標準偏差を求めよ。
データ:14 2 13 20 16

答えを見る
- 答え
 閉じる
閉じる -
分散は偏差の2乗の平均値です。この値は次の表に示すように36になります。
No. データ 偏差の2乗 1 14 1 2 2 121 3 13 0 4 20 49 5 16 9 合計 65 180 平均 13 36(=分散) 標準偏差は、分散の正の平方根なので
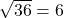 となります。
となります。
4
次のデータについて、変動係数を求めよ。
データ:1 5 2 3 5

答えを見る
- 答え
 閉じる
閉じる -
変動係数は標準偏差を平均値で割った値です。このデータは平均が3.2、標準偏差が
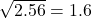 なので、変動係数は、
なので、変動係数は、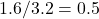 となります。
となります。No. データ 偏差の2乗 1 1 4.84 2 5 3.24 3 2 1.44 4 3 0.04 5 5 3.24 合計 16 12.8 平均 3.2(=平均) 2.56(=分散)
5
体重[kg]のデータから次の値を求めたとき、それぞれの単位を答えよ。
- 平均偏差
- 分散
- 標準偏差
- 変動係数

答えを見る
- 答え
 閉じる
閉じる -
- 平均偏差[kg]
- 分散[kg2]
- 標準偏差[kg]
- 変動係数[単位なし]
6
偏差の合計が0になることを証明せよ。

答えを見る
- 答え
 閉じる
閉じる -
n個のデータを
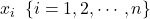 、その合計を
、その合計を 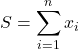 、平均値を
、平均値を 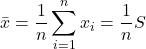 とすると、偏差の合計は次のように変形できます。
とすると、偏差の合計は次のように変形できます。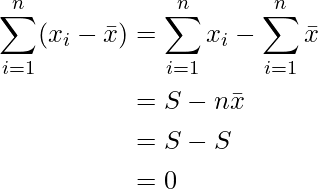
詳細については、「6-1. 分散」の【コラム】を参照してください。
7
分散よりも標準偏差の方が優れている点を述べよ。

答えを見る
- 答え
 閉じる
閉じる -
例えば、ヒトの身長を[cm]で測定した場合、平均値の単位は[cm]、分散の単位は[cm2]、標準偏差の単位は[cm]です。このとき、平均値と分散は単位が異なるため、平均値に分散を足したり、平均値から分散を引いたりすることはできません。
一方、標準偏差は平均値と単位が同じなので、平均値に標準偏差を足したり、平均値から標準偏差を引いたりすることができます。
平均値に標準偏差を足した値や平均値から標準偏差を引いた値には統計学上意味があり、後の章で詳しく説明します。
8
変動係数はどのような場合に有用か述べよ。

答えを見る
- 答え
 閉じる
閉じる -
変動係数は、標準偏差を平均値で割って求める値であるため、もともとのデータの尺度水準が比例尺度でなければなりません。名義尺度、順序尺度、間隔尺度のデータに対しては、変動係数を定義することができません。
変動係数は、同じ単位であっても桁数の異なるデータのばらつきを比較する場合に用いることができます。例えば、同じ重さ[kg]の測定であっても、ヒトの体重とマウスの体重とでは桁が異なります。このような場合、もともとのデータの桁数の影響を受けるため、標準偏差を用いてばらつきを比較することは困難です。このような場合には、変動係数を用いるとデータの桁数を気にせずにばらつきを比較することができます。
詳細については、「6-4. 変動係数」を参照してください。







