- Step1. 基礎編
- 7. 場合の数
7-1. !の使い方
数学でよく見る「!」は「階乗(かいじょう)」を表します。階乗とは「ある正の整数から1までの整数の積」のことで、「n個の異なるものを1列に並べる場合の並べ方」を計算する場合に用いられます。「n!」は次のように計算します。
例えば「5!」と書かれていた場合、これは「![]() 」を意味します。また、「5!」は下のように書くこともできます。
」を意味します。また、「5!」は下のように書くこともできます。![]() は「パイ」と読みます。
は「パイ」と読みます。
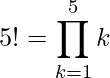
ただし、![]() の場合は「
の場合は「![]() 」となります。
」となります。
例題1:
6人を左から1列に並べる場合、何通りの並べ方があるでしょうか。

- 1人目:6人から選ばれるので6通りある
- 2人目:1人目が決まり、残りの5人から選ばれるので5通りある
- 3人目:1、2人目が決まり、残りの4人から選ばれるので4通りある
- 4人目:1、2、3人目が決まり、残りの3人から選ばれるので3通りある
- 5人目:1、2、3、4人目が決まり、残りの2人から選ばれるので2通りある
- 6人目:1、2、3、4、5人目が決まり、残りの1人なので1通りしかない
となるので、答えは「![]() 通り」となります。
通り」となります。
例題2:
4人を円卓に座らせる場合、何通りの座り方があるでしょうか。
円形に並べる場合の注意点は、回転させると同じ並びになる並べ方があるという点です。この例題では①②③④の4人が円卓に座る場合、下の4通りの座り方は円卓を回転させるとすべて同じ並びになります。

したがって、これらの並びの座り方はまとめて「1通り」としなければなりません。そこで、互いに異なるものを円形に並べる場合には「ある1ヶ所をある1つのもので固定してしまい、残りのものを並べる」と考える必要があります。ここでは、①を左上の席に固定し、残りの3席に対する②③④の3人の並べ方を考えます。

ここまでくると、先ほどの例題1のように人を1列に並べる問題と同じように考えることができます。

- 右上の席:3人から選ばれるので3通りある
- 右下の席:1人目が決まり、残りの2人から選ばれるので2通りある
- 左下の席:1、2人目が決まり、残りの1人なので1通りしかない
となるので、答えは「![]() 通り」となります。「n個の異なるものを円形に並べる場合の並べ方」は次のように計算します。
通り」となります。「n個の異なるものを円形に並べる場合の並べ方」は次のように計算します。
【コラム】②③④は固定しなくていいのか?
円卓の座り方では左上の席に①を固定させ、残りの3席に②③④の3人を座らせることを考えました。

この場合、6通りの座り方があります。

この考え方では、①の座席のみを固定させましたが、②③④を固定させた場合を考えなくてよいのかという疑問を持つかもしれません。例えば②を左上に固定した場合について考えてみます。

この並び方は全て①を左上に固定した時と一致します。
- 「A」は「お」
- 「B」は「か」
- 「C」は「え」
- 「D」は「う」
- 「E」は「あ」
- 「F」は「い」
と同じ並びになっています。したがって、円形に並べる場合には「ある1ヶ所をある1つのもので固定してしまい、残りのものを並べる」ことを考えれば十分なのです。
■おすすめ書籍
なんといってもコレ!読みやすいです。
7. 場合の数
事前に読むと理解が深まる- 学習内容が難しかった方に -
- ブログ
順列と組み合わせ








