- 7. 場合の数
練習問題(7. 場合の数)
1
次の式を計算せよ。
- 4!
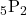
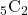

答えを見る
- 答え
 閉じる
閉じる -
- 4!=4×3×2×1=24
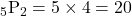
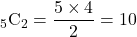
2
AさんとBさんがそれぞれさいころを1回ずつ投げる時、目の合計が8以上になるのは何通りあるか。

答えを見る
- 答え
 閉じる
閉じる -
2人のさいころの目の合計が8以上になるのは、次の組み合わせのときです。
(A, B)=(2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 3), (5, 4), (5, 5), (5, 6), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
したがって、全部で15通りとなります。
3
「1」、「1」、「2」、「3」、「4」と書かれた5枚のカードがある。これらを並べ替えて5桁の整数を作る場合、いくつの整数ができるか。

答えを見る
- 答え
 閉じる
閉じる -
5枚のカードの並べ方は「5!=120通り」です。ただし「1」と書かれたカードが2枚あるため、2つずつある重複した整数は区別せず同一のものとして考える必要があります。したがって、
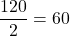 通りになります。
通りになります。
4
次の図はA町とB町を結ぶ道路を示した地図である。A町からB町へ最短距離で行く場合、何通りの道のりがあるか。ただし、途中の喫茶店に必ず寄るものとする。


答えを見る
- 答え
 閉じる
閉じる -
A町から喫茶店に行くまでの道のりは「右」に3区画、「上」に4区画あることから、これらの組み合わせは
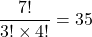 通りとなります。同様に、喫茶店からB町に行くまでの道のりは「右」に2区画、「上」に3区画あることから、これらの組み合わせは
通りとなります。同様に、喫茶店からB町に行くまでの道のりは「右」に2区画、「上」に3区画あることから、これらの組み合わせは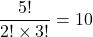 通りとなります。
通りとなります。これらを合わせると
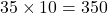 通りとなります。
通りとなります。
5
6種類の宝石を使ってブレスレットを作るとき、宝石の並べ方は何通りあるか。

答えを見る
- 答え
 閉じる
閉じる -
このような問題は「数珠順列」と呼ばれます。円に並べる順列(円順列)と似ていますが、ブレスレットは裏表をひっくり返したときに同じ並び方が現れる点に注意しなくてはなりません。
6つの宝石を円形に並べる方法は
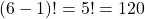 通りです。ただし、裏表をひっくり返すと同一となる並び方が2つずつ含まれるため、これらを区別せず同一のものとして考える必要があります。したがって、
通りです。ただし、裏表をひっくり返すと同一となる並び方が2つずつ含まれるため、これらを区別せず同一のものとして考える必要があります。したがって、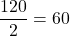 通りになります。
通りになります。







