- Step1. 基礎編
- 7. 場合の数
7-3. Cの使い方
「![]() 」と並んで出てくるものに「
」と並んで出てくるものに「![]() 」があります。これは「組み合わせ(Combination)」を表します。組み合わせとは「異なるn個のものからr個を取り出す」ことです。このときの取り出し方の組み合わせ総数は次のように計算します。
」があります。これは「組み合わせ(Combination)」を表します。組み合わせとは「異なるn個のものからr個を取り出す」ことです。このときの取り出し方の組み合わせ総数は次のように計算します。
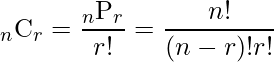
「![]() 」はある集団からいくつかを取り出してそれを取り出した順に並べる場合に使いますが、「
」はある集団からいくつかを取り出してそれを取り出した順に並べる場合に使いますが、「![]() 」はある集団からいくつかを取り出す(ただし並べたりしない)場合に使います。例えば
」はある集団からいくつかを取り出す(ただし並べたりしない)場合に使います。例えば![]() と書かれていた場合、これは「異なる5個のものから2個取り出す」ことを意味し、「
と書かれていた場合、これは「異なる5個のものから2個取り出す」ことを意味し、「![]() 通り」と計算されます。
通り」と計算されます。
また、次に示すように「![]() 」となります。
」となります。
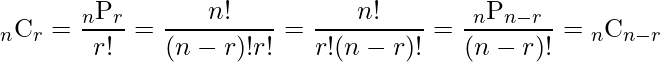
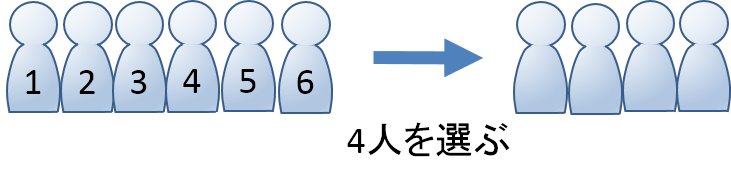
例題1:
6人のグループから4人を選ぶ場合、何通りの選び方があるでしょうか。
- 1人目:6人から選ばれるので6通りある
- 2人目:1人目が決まり、残りの5人から選ばれるので5通りある
- 3人目:1、2人目が決まり、残りの4人から選ばれるので4通りある
- 4人目:1、2、3人目が決まり、残りの3人から選ばれるので3通りある
ただし、選ばれた4人は並べ方を考えなくてよいので、4人を並べたとしたときの4!通りの並べ方は全て同じものと考えることができます。したがって、「6人から4人を選んでその順に並べる![]() 」を「4人の並べ方4!」で割ることで、
」を「4人の並べ方4!」で割ることで、![]() を算出できます。すなわち、
を算出できます。すなわち、![]() 通りとなります。
通りとなります。
例題2:
1から9までの数字から、4つを取り出して小さい順に並べる場合、何通りの並べ方があるでしょうか。
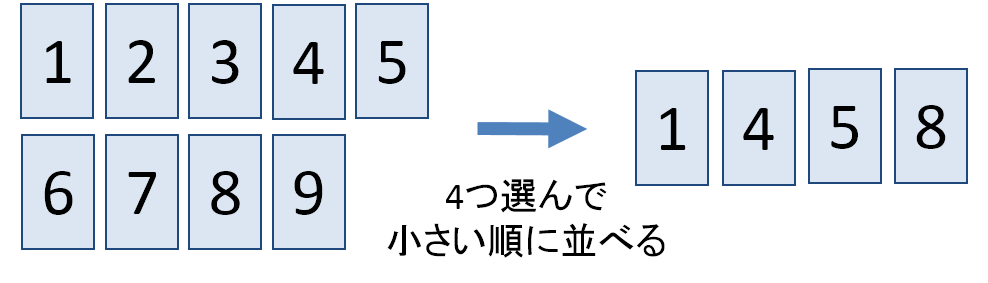
この問題では「取り出して並べるからPを使えばいい」と早合点してはいけません。取り出した4つの数字を小さい順に並べる並べ方はどのような場合でも1通りしかありません。つまり「ある集団からいくつか取り出して並べる」と考えるのではなく、「ある集団からいくつかを取り出す」と考えなくてはなりません。
したがって、「![]() 」を使って答えを算出します。すなわち、
」を使って答えを算出します。すなわち、![]() 通りとなります。
通りとなります。
例題3:
10人のグループを4人、3人、3人の計3グループに分ける場合、何通りの分け方があるでしょうか。
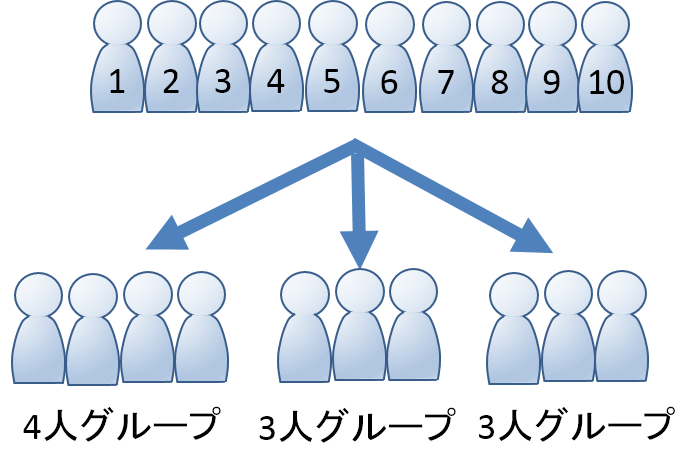
この問題も、グループ内での並べ方を考える必要がはないので「C」を使います。
- 4人グループ:10人から4人を選ぶ選び方は、
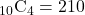 通りある
通りある - 3人グループ1つ目:残りの6人から3人を選ぶ選び方は、
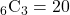 通りある
通りある - 3人グループ2つ目:残り3人で3人グループとなるので、これは1通である
ただし、2つの3人グループは区別をしないため、例えばABCDEFの6人がABC(3人グループ1つ目)とDEF(3人グループ2つ目)と分かれる場合と、DEF(3人グループ1つ目)とABC(3人グループ2つ目)と分かれる場合は同じものとして考える必要があります。よって、答えは![]() 通りとなります。
通りとなります。
■おすすめ書籍
やっぱりコレ!読みやすいので超おすすめです。
7. 場合の数
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 7. 場合の数
7-1. !の使い方
- 7. 場合の数
7-2. Pの使い方
- ブログ
順列と組み合わせ








