Step1. 基礎編
7. 場合の数

7-2. Pの使い方

数学でよく見る「 ${}_{\bigcirc} \mathrm{P}_{\triangle}$ 」は「順列（Permutation）」を表します。順列とは、「異なるn個からr個を取り出した順に1列に並べる」ことです。このときの並べ方の総数は次のように計算します。

${}_n \mathrm{P}_{r}= n \times (n-1) \times (n-2) \times \dots \times (n-r+1)$

例えば、 ${}_5 \mathrm{P}_{2}$ と書かれていた場合、これは「異なる5個のものから2個を取り出して、取り出した順に並べる」ことを意味し、「 ${}_5 \mathrm{P}_{2}=5 \times 4 = 20$ 」と計算されます。

例題1：

6人のグループから4人を選び、選ばれた順番に左から1列に並べる場合、何通りの並び方があるでしょうか。

Pの使い方1

1人目：6人から選ばれるので6通りある
2人目：1人目が決まり、残りの5人から選ばれるので5通りある
3人目：1、2人目が決まり、残りの4人から選ばれるので4通りある
4人目：1、2、3人目が決まり、残りの3人から選ばれるので3通りある

ここまでで4人が並びました。したがって、 ${}_6 \mathrm{P}_{4}=6\times 5 \times 4 \times 3=360$ 通りとなります。

例題2：

A社5人とB社4人のグループで会議をします。司会者1名をA社から、タイムキーパー1名と書記1名をそれぞれB社から選ぶことにします。このとき、3つの役割に割り振られる人の組み合わせは全部で何通りあるでしょうか。

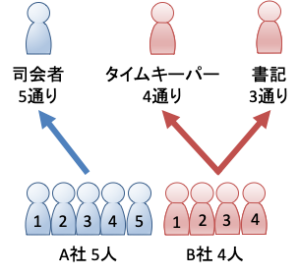
まず、A社の司会者について考えます。司会者はA社5人から選ばれるので、 ${}_5 \mathrm{P}_1=5$ 通りとなります。

次にB社のタイムキーパーと書記について考えます。

書記：B社4人から選ばれるので4通りある
タイムキーパー：残りのB社3人から選ばれるので3通りある

これらをまとめると ${}_4 \mathrm{P}_2 =4 \times 3 =12$ 通りとなります。最後に、A社の組み合わせとB社の組み合わせを合わせて考えればよいので、 ${}_5 \mathrm{P}_1 \times {}_4 \mathrm{P}_2=5 \times 12=60$ 通りとなります。