- Step1. 基礎編
- 11. 確率変数と確率分布
11-3. 連続型確率分布
連続型変数は、重さや温度などのように連続した値をとるものを指します。例えば重さの場合、50kgと51kgの間には50.5kgや50.1kg、50.000001kgなど無数の値が存在します。

連続型変数の取りうる値に対応する確率が存在する場合、この変数を「連続型確率変数」といいます。確率変数が連続型である場合の確率分布を「連続型確率分布」、あるいは「連続型分布」といいます。
例題:
連続型確率変数![]() がとる値を、1から6までの実数とします。
がとる値を、1から6までの実数とします。![]() がどの数値を取る確率も等しいとき、
がどの数値を取る確率も等しいとき、![]() となる確率はいくらでしょうか。
となる確率はいくらでしょうか。

11‐2章の離散型確率変数のときと同様に考えて![]() としてしまうのは誤りです。連続型分布では、確率変数の値をある一点に定めた場合にその値をとる確率は「0」になる、というのが正しい答です。
としてしまうのは誤りです。連続型分布では、確率変数の値をある一点に定めた場合にその値をとる確率は「0」になる、というのが正しい答です。
連続型確率変数の場合、1から6までで![]() が取りうる値は無限にあります。例えば、1と1.1の間には1.01や1.00001といった値が無限に存在します。Xがどの値を取る確率も等しい時、それぞれの確率は全て足し合わせると1であり、また
が取りうる値は無限にあります。例えば、1と1.1の間には1.01や1.00001といった値が無限に存在します。Xがどの値を取る確率も等しい時、それぞれの確率は全て足し合わせると1であり、また![]() は無限に存在する値のうちのある一点であることから、
は無限に存在する値のうちのある一点であることから、![]() は次のように「0」となるのです。
は次のように「0」となるのです。
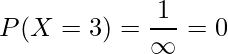
11. 確率変数と確率分布
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 11. 確率変数と確率分布
11-2. 離散型確率分布と確率質量関数
- ブログ
確率変数とは







