- 11. 確率変数と確率分布
練習問題(11. 確率変数と確率分布)
1
次の中から、離散型変数を選べ。
- ある成人男性の体重X
- 10枚のコインを投げて、表になる枚数X
- ある書籍のページ数X
- 大気中の湿度X
- お酒の中のアルコール度数X
- 1枚の歪みのないコインで表が出るまで連続で投げた回数X

答えを見る
- 答え
 閉じる
閉じる -
連続型変数は、重さや温度などのように連続した値をとるものを指します。1, 4, 5は連続した値をとる変数であり、ある値と他の値の間に無数の値があると考えられるので連続型変数です。
よって、残った選択肢である「2, 3, 6」が離散型変数となります。
2
確率質量関数 ![]() と確率密度関数を
と確率密度関数を ![]() について、次の4つの中から正しい記述を選べ。
について、次の4つの中から正しい記述を選べ。
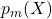 は、Xの値によっては負になることがある。
は、Xの値によっては負になることがある。- 確率質量関数
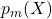 は、1を超えることがある。
は、1を超えることがある。 - 確率密度関数
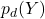 は、1を超えることがある。
は、1を超えることがある。 - どちらも0.4で値が存在するとき、
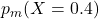 と
と 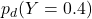 はどちらも確率となる。
はどちらも確率となる。

答えを見る
- 答え
 閉じる
閉じる -
- ×:確率質量関数も確率密度関数も負になることはありません。
- ×:確率質量関数
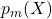 はそれぞれの
はそれぞれの  に対応する値が確率そのものであるため、1を超えることはありません。
に対応する値が確率そのものであるため、1を超えることはありません。 - ◯:確率密度関数
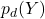 はそれぞれの
はそれぞれの 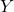 に対応する値が確率ではなく確率密度であるため、1を超えることがあります。
に対応する値が確率ではなく確率密度であるため、1を超えることがあります。 - ×:確率密度関数のある一点における値は確率ではありません。
3
次のような確率密度関数があるとき、![]() となる確率はいくらになるか。
となる確率はいくらになるか。
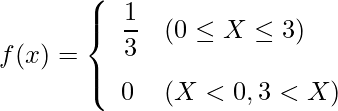

答えを見る
- 答え
 閉じる
閉じる -
Xが3より大きい領域については
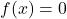 なので、考える必要はありません。したがって、積分を使って次のように計算すると
なので、考える必要はありません。したがって、積分を使って次のように計算すると になります。
になります。![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle P(1 \leq X \leq 4) &=& \displaystyle \int_1^4 f(x)dx \\ \vspace{8mm} &=& \displaystyle \int_1^3 \frac{1}{3} dx + \displaystyle \int_3^4 0 dx \\ \vspace{8mm} &=& \displaystyle \int_1^3 \frac{1}{3} dx \\ \vspace{8mm} &=& \left[ \displaystyle \frac{1}{3}x \right]_1^3 = \displaystyle \frac{1}{3} \times 3 - \displaystyle \frac{1}{3} \times 1 \\ \vspace{8mm} &=& \displaystyle 1- \frac{1}{3} \\ \vspace{8mm} &=& \displaystyle \frac{2}{3} \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-34d0b6710be925072cab9d95de74cd49_l3.png)
4
次のような確率密度関数があるとき、![]() となる確率はいくらになるか。
となる確率はいくらになるか。
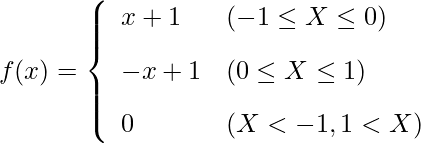

答えを見る
- 答え
 閉じる
閉じる -
積分を使って次のように計算すると
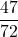 になります。
になります。![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle P(\displaystyle -\frac{1}{2} \leq X\leq \displaystyle \frac{1}{3}) &=& \displaystyle \int_{-\frac{1}{2}}^{\frac{1}{3}} f(x)dx \\ \vspace{8mm} &=& \displaystyle \int_{-\frac{1}{2}}^0 (x+1) dx + \displaystyle \int_0^\frac{1}{3} (-x+1) dx \\ \vspace{8mm} &=& \left[ \displaystyle \frac{1}{2}x^2+x \right]_{-\frac{1}{2}}^0 + \left[ \displaystyle -\frac{1}{2}x^2+x \right]_0^\frac{1}{3} \\ \vspace{8mm} &=& - \left\{ \displaystyle \frac{1}{2} \times \left(-\frac{1}{2}\right)^2 - \displaystyle \frac{1}{2} \right\} + \displaystyle \left(-\frac{1}{2}\right) \times \left(-\frac{1}{3}\right)^2 + \frac{1}{3} \\ \vspace{8mm} &=& \displaystyle -\frac{1}{8} + \frac{1}{2} -\frac{1}{18} + \frac{1}{3} \\ \vspace{8mm} &=& \displaystyle \frac{47}{72} \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-f0cd18e677b33bc37c47de6b8d1eb4c6_l3.png)
5
さいころを1回投げて、その時出る目Xを確率変数とする。ただし、このさいころのそれぞれの目が出る確率は一定ではなく、出る目に比例するとする。
つまり、ある定数![]() を用いて
を用いて![]() の目が出る確率
の目が出る確率![]() が次のように表すことができるものとする。
が次のように表すことができるものとする。
これが確率分布となるための![]() の値を求めよ。
の値を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
確率分布の約束である、全事象
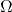 に対して
に対して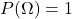 となるよう
となるよう を決定します。なお、全ての
を決定します。なお、全ての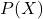 について
について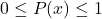 となることから、必ず
となることから、必ず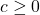 になります。さいころのどの目が出るかについては排反な事象であるため、次の等式が成り立ちます。
になります。さいころのどの目が出るかについては排反な事象であるため、次の等式が成り立ちます。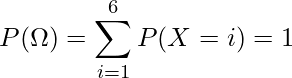
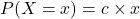 と表されることから、この式は次のように変形できます。
と表されることから、この式は次のように変形できます。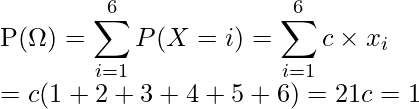
よって、
 の値は
の値は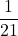 と求められます。
と求められます。







