- Step1. 基礎編
- 11. 確率変数と確率分布
11-4. 確率密度と確率密度関数
■確率密度
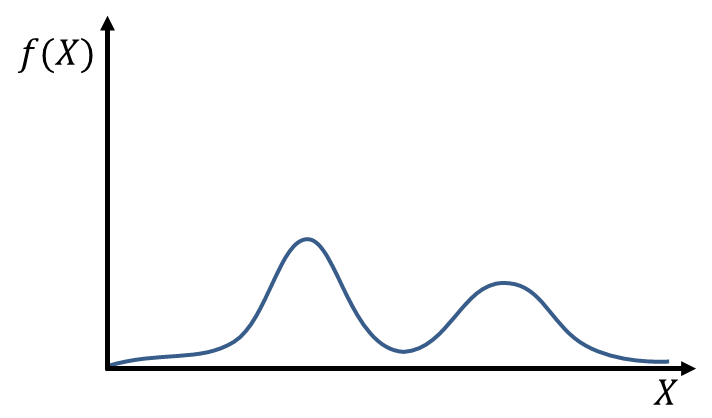
次の図は連続型確率分布のイメージを表したものです。横軸は確率変数![]() を表します。11‐3章で学んだように、連続型確率変数の場合には確率変数がある一点の値をとる確率は0になることから、縦軸は確率ではなく「確率密度」というものを使います。確率密度は定義域内での
を表します。11‐3章で学んだように、連続型確率変数の場合には確率変数がある一点の値をとる確率は0になることから、縦軸は確率ではなく「確率密度」というものを使います。確率密度は定義域内での![]() の値の「相対的な出やすさ」を表すものです。
の値の「相対的な出やすさ」を表すものです。
■確率密度関数
連続型確率変数Xがある値xをとる確率密度を関数![]() とすると、
とすると、![]() を「確率密度関数」と呼びます。確率とは異なり、
を「確率密度関数」と呼びます。確率とは異なり、![]() になる場合もあります。
になる場合もあります。
例題1:
確率変数![]() がとる値
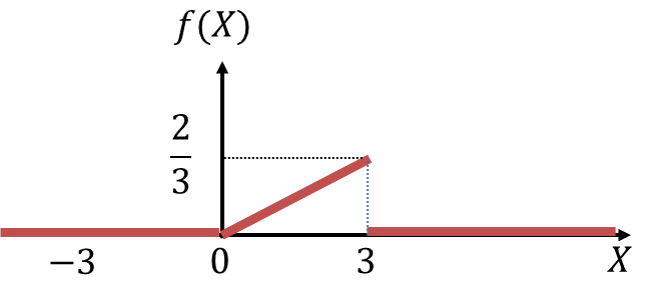
がとる値![]() が0から3までの実数を取る場合に、次のような確率密度関数
が0から3までの実数を取る場合に、次のような確率密度関数![]() を定義します。この関数からどのようなことが言えるでしょうか。
を定義します。この関数からどのようなことが言えるでしょうか。
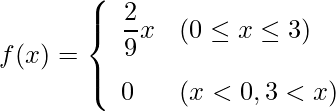
![]() と
と![]() の値を求めると次のようになります。
の値を求めると次のようになります。
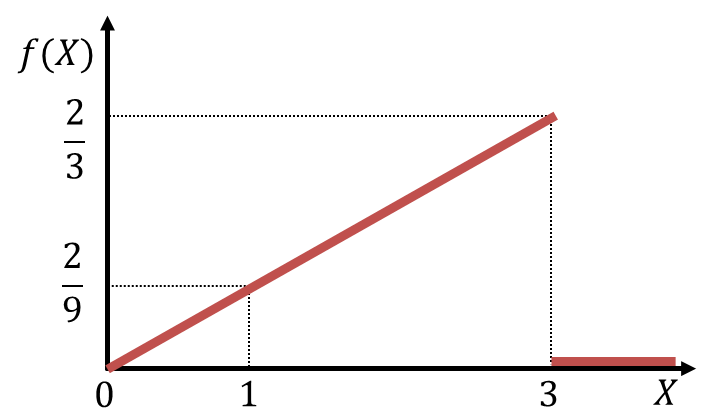
![]() であることから、この確率密度関数は1よりも3が「相対的に出やすい」ことが分かります。また、「確率密度関数が右肩上がり」=「
であることから、この確率密度関数は1よりも3が「相対的に出やすい」ことが分かります。また、「確率密度関数が右肩上がり」=「![]() が大きくなるほど確率密度も高い」=「高い値が出やすい」と読み取ることもできます。
が大きくなるほど確率密度も高い」=「高い値が出やすい」と読み取ることもできます。![]() や
や![]() といった
といった![]() の領域については、そのような値が出ない(=そのような値になり得ない)ことを表しています。
の領域については、そのような値が出ない(=そのような値になり得ない)ことを表しています。
例題2:
次のような確率密度関数からどのようなことが言えるでしょうか。
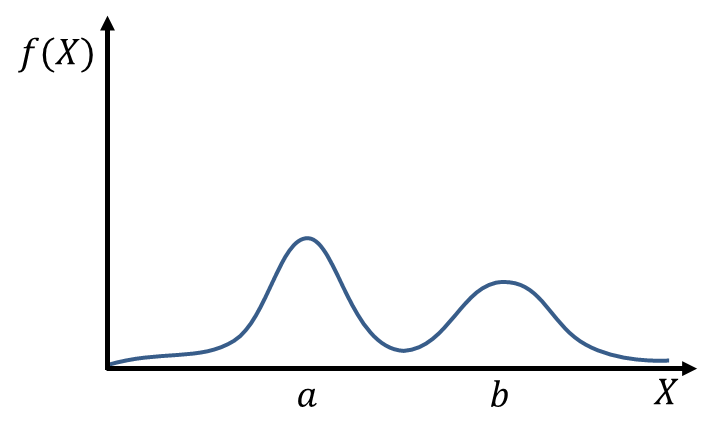
この確率密度関数には、![]() が
が![]() と
と![]() のあたりに山が二つあります。つまり、「他の値よりも
のあたりに山が二つあります。つまり、「他の値よりも![]() や
や![]() の近くの値が出やすい」ことが分かります。また、
の近くの値が出やすい」ことが分かります。また、![]() の方の山が高いことから「
の方の山が高いことから「![]() と
と![]() を比べると、
を比べると、![]() に近い値の方がより出やすい」ということも読み取れます。
に近い値の方がより出やすい」ということも読み取れます。
11. 確率変数と確率分布
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 11. 確率変数と確率分布
11-3. 連続型確率分布
- ブログ
確率変数とは






