- Step1. 基礎編
- 11. 確率変数と確率分布
11-1. 確率変数と確率分布
■確率変数
「確率変数」は、ある変数の値をとる確率が存在する変数のことです。例えば、さいころを投げて出る目は{1, 2, 3, 4, 5, 6}のいずれかであり、それぞれの目が出る確率は![]() であることから、さいころを投げて出る目は確率変数であると言えます。
であることから、さいころを投げて出る目は確率変数であると言えます。

この場合、確率変数の値(=さいころの出る目)を![]() とおくと次のように表すことができます。右側のカッコの中は
とおくと次のように表すことができます。右側のカッコの中は![]() がとる値の範囲であり、この例では「確率変数
がとる値の範囲であり、この例では「確率変数![]() が1から6までの整数の値を取る」ことを表しています。
が1から6までの整数の値を取る」ことを表しています。
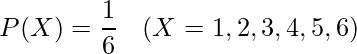
例えば「さいころを投げて3の目が出る事象の確率は![]() である」ことは、次のいずれかのように書くことができます。
である」ことは、次のいずれかのように書くことができます。
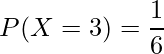
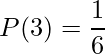

さいころの場合、出る目の値をそのまま確率変数がとる値とすることができますが、事象に数字がない場合でも、それぞれ事象に数値を設定することで確率変数がとる値とすることができます。例えば1枚のコインを投げる場合に、表が出る事象に「1」を、裏が出る事象に「0」を対応させると、確率変数になります。
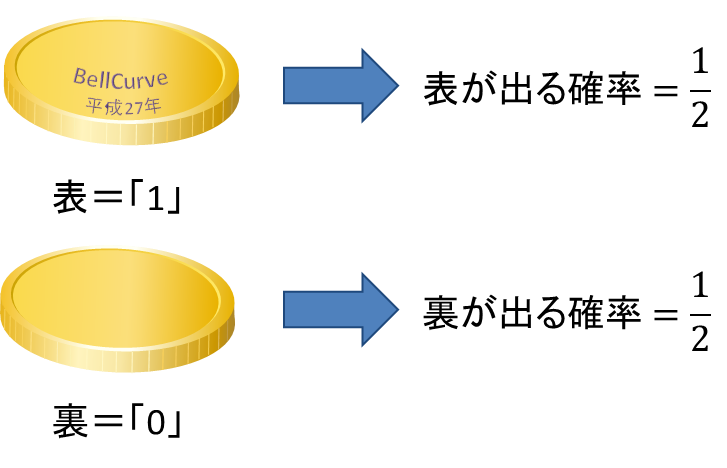
表が出る事象も裏が出る事象のどちらも確率は![]() であることから、確率変数
であることから、確率変数![]() を用いて次のように書けます。
を用いて次のように書けます。
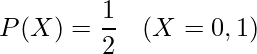
■確率分布
確率変数がとる値とその値をとる確率の対応の様子を「確率分布」と言います。例えば、さいころを投げる例では、1から6までの確率変数の値にそれぞれ![]() という確率が対応しているので、確率分布と言えます。
という確率が対応しているので、確率分布と言えます。
| さいころの出る目の確率分布 | ||||||
|---|---|---|---|---|---|---|
| さいころの出る目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 確率 | ||||||
コインを投げる例では、0と1の確率変数の値にそれぞれ![]() という確率が対応しているので、同様に確率分布と言えます。
という確率が対応しているので、同様に確率分布と言えます。
| コインの出る目の確率分布 | ||
|---|---|---|
| コインの裏表 | 表(=1) | 裏(=0) |
| 確率 | ||
■おすすめ書籍
このあたりの章までの復習にちょうどよいです。
11. 確率変数と確率分布
事前に読むと理解が深まる- 学習内容が難しかった方に -
- ブログ
確率変数とは







