- Step1. 基礎編
- 11. 確率変数と確率分布
11-6. 連続型確率分布と確率2
例題:
連続型確率変数![]() がとる値の範囲を、0から6までの実数とします。
がとる値の範囲を、0から6までの実数とします。![]() がどの数値を取る確率も等しいとき、
がどの数値を取る確率も等しいとき、![]() となる確率はいくらでしょうか。
となる確率はいくらでしょうか。
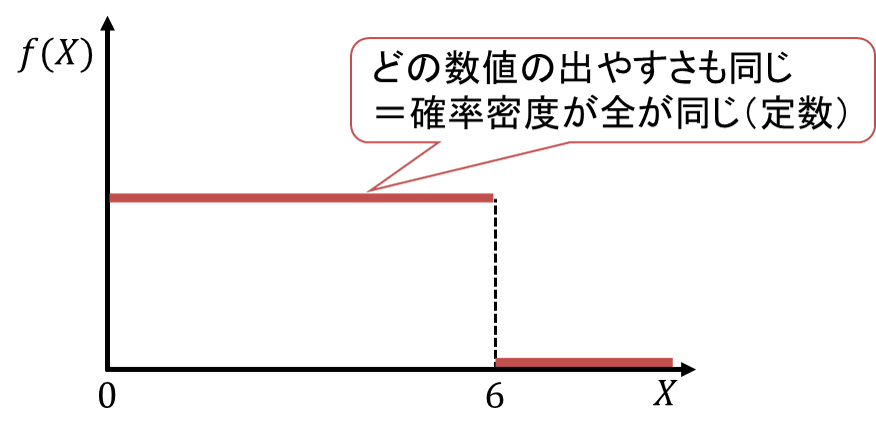
この問題では確率密度関数![]() が分からないので、まず確率密度関数を求めます。「0から6までのどの数値を取る確率も等しい=0から6までの確率密度は全て等しい」ことから、この確率密度をcとおくと確率密度関数
が分からないので、まず確率密度関数を求めます。「0から6までのどの数値を取る確率も等しい=0から6までの確率密度は全て等しい」ことから、この確率密度をcとおくと確率密度関数![]() は次のように表すことができます。
は次のように表すことができます。
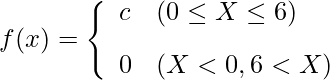

cの値を求めるために、11-5章で学んだ「確率密度関数![]() と(横軸)
と(横軸)![]() 軸で囲まれる部分の面積は1である」ことを用います。
軸で囲まれる部分の面積は1である」ことを用います。
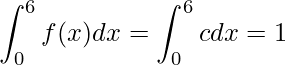
この式を計算すると次のようになります。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle \int_0^6 f(x)dx &=& \left[ cx \right]_0^6 \\ &=& c \times 6 - c \times 0 =6c=1\\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-b1de7f203e515b9749391bdcc496a2d2_l3.png)
したがって、
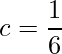
となります。つまり、![]() が求める確率密度関数です。この
が求める確率密度関数です。この![]() を用いて
を用いて![]() となる確率
となる確率![]() を計算します。
を計算します。![]() は、下図の青色の部分の面積です。
は、下図の青色の部分の面積です。
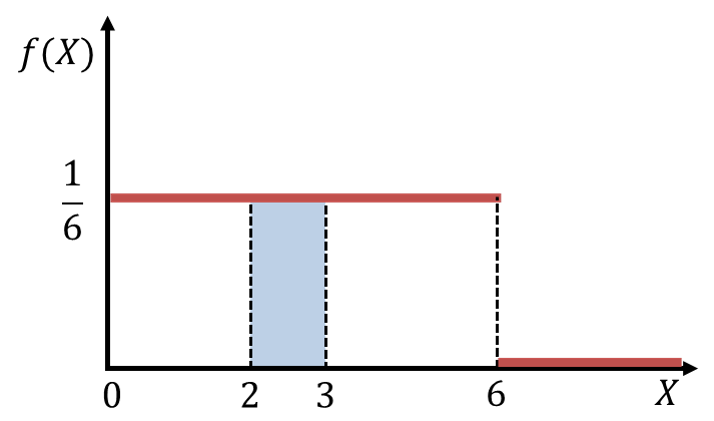
![Rendered by QuickLaTeX.com \begin{eqnarray*} P(2 \leq X \leq 3) &=& \displaystyle \int_2^3 \displaystyle \frac{1}{6} dx \\ &=& \left[ \displaystyle \frac{1}{6}x \right]_2^3 \\ &=& \displaystyle \frac{1}{6} \times 3 - \displaystyle \frac{1}{6} \times 2 \\ &=& \displaystyle \frac{1}{6}\\ \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-03dd78842c6b5ec5d0e32e7535482971_l3.png)
したがって、求める確率は![]() となります。
となります。
【コラム】様々な確率分布
離散型分布と連続型分布の種類を示したものが下の表です。これらの分布の詳細は、以降の章で解説します。また、確率分布はこの表にのっているもの以外にもたくさんの種類があります。
| 離散型分布 | 連続型分布 |
|---|---|
| 一様分布 二項分布 多項分布 ポアソン分布 幾何分布 (超幾何分布) | 連続一様分布 正規分布 指数分布 t分布 F分布 カイ二乗分布 |
11. 確率変数と確率分布
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 11. 確率変数と確率分布
11-5. 連続型確率分布と確率1







