- Step1. 基礎編
- 11. 確率変数と確率分布
11-5. 連続型確率分布と確率1
確率密度関数の場合、確率変数がある一点の値をとる確率は0になることから、”ある範囲”をとることで確率を求められます。ある確率密度関数![]() において、
において、![]() (確率変数
(確率変数![]() がとる値の範囲が
がとる値の範囲が![]() 以上
以上![]() 以下)となる確率は次の積分の計算によって求められます。
以下)となる確率は次の積分の計算によって求められます。
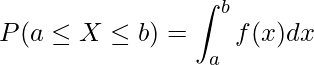
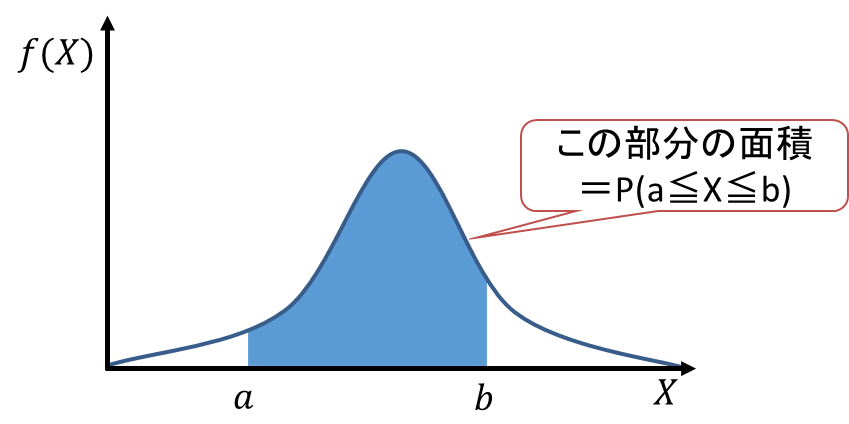
この積分では、![]() の範囲における確率密度関数
の範囲における確率密度関数![]() (次の図の青色の曲線)、横軸の
(次の図の青色の曲線)、横軸の![]() 軸、
軸、![]() 、
、![]() で囲まれる面積(次の図の青色の部分)を算出しています。
で囲まれる面積(次の図の青色の部分)を算出しています。
確率の約束の1つとして、「全事象が起こる確率は1である」ことは9‐1章で既に学びました。連続型確率分布では次のように表すことができます。
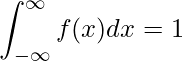
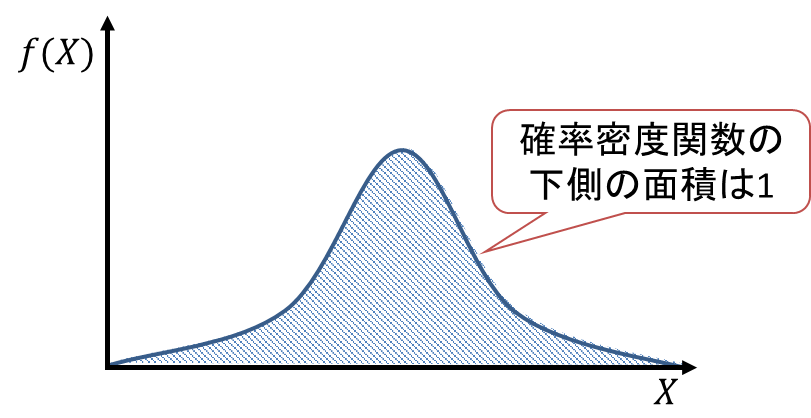
これは、「確率密度関数![]() と
と![]() 軸(横軸)で囲まれる部分全体の面積は1である」ことを意味します。
軸(横軸)で囲まれる部分全体の面積は1である」ことを意味します。
例題:
次のような確率密度関数があるとき、![]() となる確率はいくらでしょうか。
となる確率はいくらでしょうか。
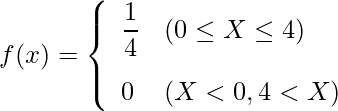
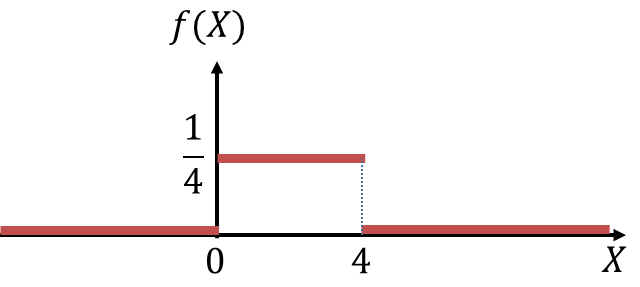
この確率密度関数を図示すると、次のようになります。
![]() は、次のグラフの青色の部分の面積です。
は、次のグラフの青色の部分の面積です。
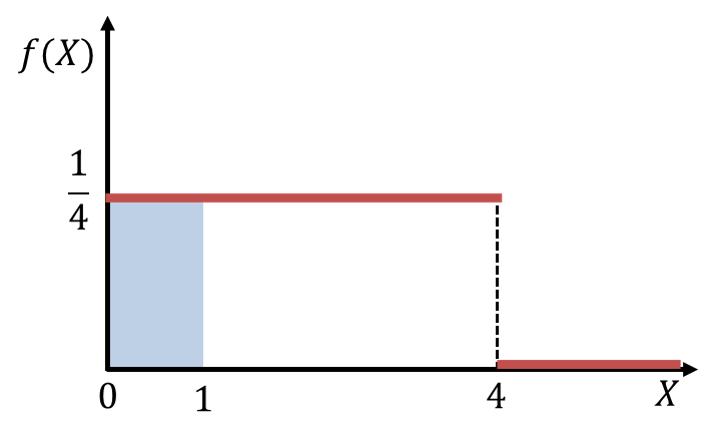
この部分の面積は、積分を使って次のように計算すると![]() になります。
になります。
![Rendered by QuickLaTeX.com \begin{eqnarray*} \displaystyle P(0 \leq X \leq 1) &=& \displaystyle \int_0^1 f(x)dx \\ \vspace{8mm} &=& \displaystyle \int_0^1 \displaystyle \frac{1}{4}dx \\ \vspace{8mm} &=& \left[ \displaystyle \frac{1}{4}x \right]_0^1 = \displaystyle \frac{1}{4} \times 1 - \displaystyle \frac{1}{4} \times 0 \\ \vspace{8mm} &=& \displaystyle \frac{1}{4} \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-de168092579edafacabf7ef1b4a5db2e_l3.png)
11. 確率変数と確率分布
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 9. 確率と期待値
9-1. 確率
- 11. 確率変数と確率分布
11-3. 連続型確率分布
- ブログ
確率変数とは







