「確率」は、物事の「起こりやすさ」を定量的に表す指標です。「起こりやすさ」の指標は「絶対に起こらない」から「絶対に起こる」の間にあります。確率では、「絶対に起こらない」ことには「0」が、「絶対に起こる」ことには「1」がそれぞれ対応します。

例えば日常生活でよく目にする確率に、「降水確率」や「宝くじの当選確率」があります。

• 今日の降水確率：0%、30%、80％など
• 宝くじで1等が当たる確率：0.001%、0.0001%など

この確率を元に、「雨が振りそうだから傘を持って行ったほうがいい」や「当選する確率が低そうだからこの宝くじを買うのはやめておこう」といった将来を予測して、行動や意思を決めることもできます。

確率はPを用いて表します。このPは確率を表す英単語「Probability」の頭文字です。ある事象について、その事象が起こる確率は次のように表します。

P(ある事象)：「ある事象」が起こる「確率」

例えば、さいころを1回投げる場合において、事象Aを「偶数の目が出る」事象とします。このとき、「」は「偶数の目が出る確率」を表します。

確率には次の3つの約束ごと（公理）があります。

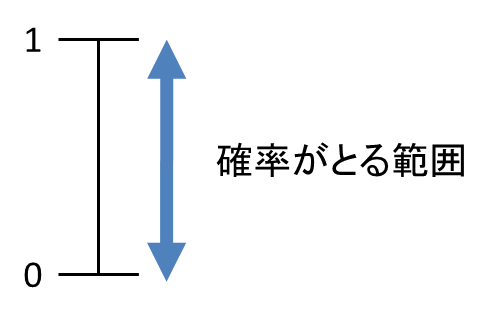
1. どのような事象についての確率も、0以上1以下となる

確率は、負の数になったり１を超えたりすることは絶対にありません。

2. 「全事象」を「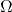」と表すと、全事象の起こる確率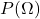は1となる

例えば、さいころを1回投げるとき、全事象は「出る目が1, 2, 3, 4, 5, 6となる」事象です。これらの事象のうち、いずれかの目が出る確率は1となります。

3. 互いに排反な事象の和集合の確率は、それぞれの事象の確率の和となる

例えば、1つのさいころを1回投げるとき、1の目と2の目が同時に出ることはないため、これらの事象は排反事象です。したがってその和事象である「1または2の目が出る」確率は、次のように計算できます。

P(1または2が出る)＝P(1が出る)+P(2が出る)

【コラム】事象Aの確率「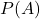」の書き方

事象Aの確率はと書くと説明しましたが、書籍によってはと書かれていることがあります。これはと同じく、事象Aの確率を表しています。

■おすすめ書籍

統計を学び始めた時に読みました。統計を学ぶ取っ掛かりにはとても良かったです。この本を読んでおくと、このあとに少し難しい本を読んでもついていけるかと思います。