- Step1. 基礎編
- 9. 確率と期待値
9-3. 確率の計算(順列・組み合わせ)
確率の計算を行う場合、場合の数で学んだ組み合わせ(C)や順列(P)、あるいは集合の考え方を用いることでより効率よく計算できます。
例題:
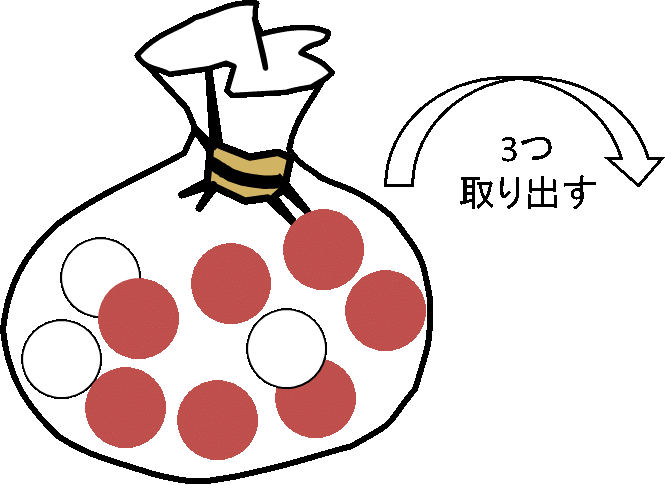
白いボール3個と赤いボール7個があります。この中から無作為にボールを3つ取り出すとき、次のような事象が起こる確率はいくらでしょうか。
- 全て赤いボールが取り出される
- 白いボールが1つ、赤いボールが2つ取り出される
1. 全て赤いボールが取り出される
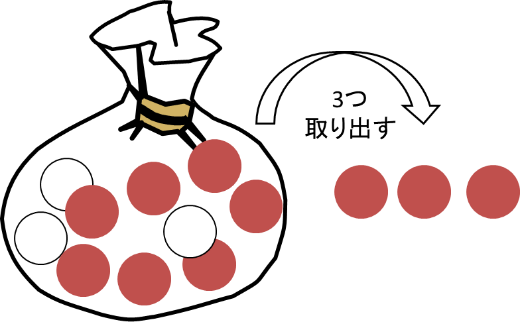
ボールは全部で10個あり、その中から3つ取り出す組み合わせは全部で![]() 通りあります。全て赤いボールが取り出される組み合わせは、全部で7つある赤いボールから3つ取り出される場合です。これは
通りあります。全て赤いボールが取り出される組み合わせは、全部で7つある赤いボールから3つ取り出される場合です。これは![]() 通りあります。したがって、求める確率は次のようになります。
通りあります。したがって、求める確率は次のようになります。
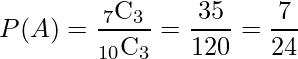
2. 白いボールが1つ、赤いボールが2つ取り出される
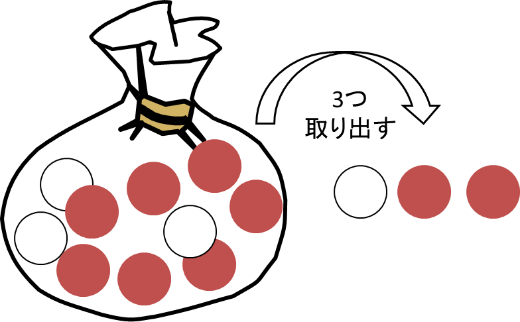
白いボールが1つ、赤いボールが2つ取り出される組み合わせは、全部で3つある白いボールから1つ、全部で7つある赤いボールから2つが取り出される場合です。
- 3つある白いボールから1つ取り出される→
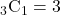 通り
通り - 7つある赤いボールから2つ取り出される→
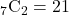 通り
通り
したがって、求める確率は次のようになります。
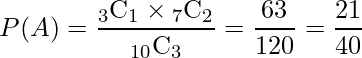
■おすすめ書籍
場合の数から確率に特化しています。イラストが多いのもGood!
9. 確率と期待値
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 7. 場合の数
7-1. !の使い方
- 7. 場合の数
7-2. Pの使い方
- 7. 場合の数
7-3. Cの使い方
- 8. さまざまな事象
8-1. 事象とは
- ブログ
順列と組み合わせ








