例題：

白いボール3個と赤いボール7個があります。この中から無作為にボールを3つ取り出すとき、赤いボールが少なくとも1つ取り出される確率はいくらでしょうか。

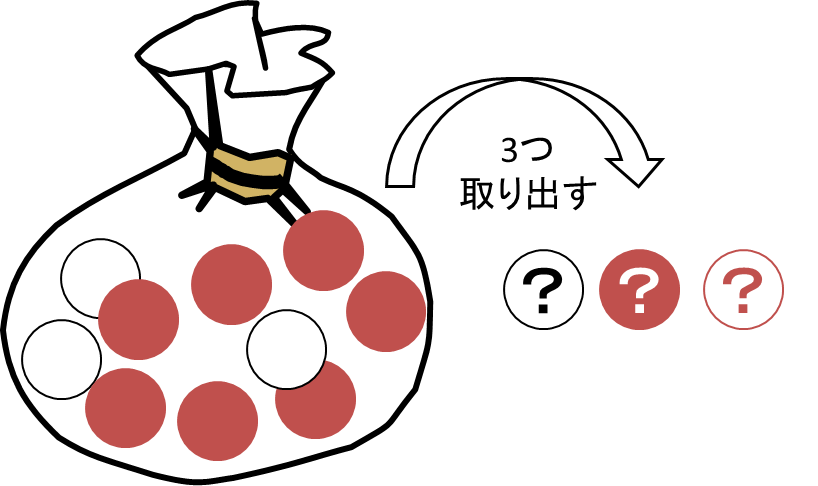
■場合分けする場合

赤いボールが「少なくとも1つ」出てくる場合は、このままだと何通りあるか計算するのは難しいので、次のようにいくつかの場合に分けて考えます。

1. 赤いボールが1つ取り出される
2. 赤いボールが2つ取り出される
3. 赤いボールが3つ取り出される

これに白いボールが取り出される数を組み合わせると次のようになります。

1. 白いボールが2個取り出され、赤いボールが1つ取り出される
2. 白いボールが1個取り出され、赤いボールが2つ取り出される
3. 赤いボールが3つ取り出される

1. 「白いボールが2個取り出され、赤いボールが1つ取り出される」について
• 3つある白いボールから2つ取り出される→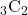通り
• 7つある赤いボールから1つ取り出される→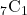通り

となることから、通りです。

2. 「白いボールが1個取り出され、赤いボールが2つ取り出される」について

1と同様に考えればよいので通りとなります。

3. 「赤いボールが3つ取り出される」について

通りとなります。

1, 2, 3の結果をまとめると、



となることから、



と計算できます。よって、求める確率はとなります。

■余事象を用いる場合

「少なくとも◯個～」等と表される場合は、余事象を考えると計算が簡単になることがあります。「赤いボールが少なくとも1つ取り出される」事象の余事象は、「赤いボールが1つも取り出されない」＝「白いボールが3つ取り出される」です。これは通りしかありません。

事象と余事象の関係から、ある事象をA、その余事象を、全事象をとすると

が成り立つので、赤いボールが少なくとも1つ取り出される事象は、

通りです。以上の事から、求める確率はとなります。余事象の確率は、ある事象Aの確率を用いて次のように求められます。