ある試行において、根元事象（こんげんじしょう）がn個存在し、そのうち事象Aに含まれる根元事象が全部でk個あるとき、事象Aが起こる確率を次のように定義します。これをラプラスの定義（古典的定義）といいます。

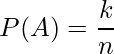
事象の確率を求める時には、「根元事象は同様に確からしい」という前提が置かれます。これは「どの事象が起こる確率も等しい」ということを表しています。例えばさいころを投げる場合、それぞれの目が出る確率は「同様に確からしい」ので、

P(1の目が出る)＝P(2の目が出る)=P(3の目が出る)=P(4の目が出る)=P(5の目が出る)=P(6の目が出る)

という関係が成り立ちます。

さいころを1回投げるとき、出る目は「1, 2, 3, 4, 5, 6」の6種類あることから、根元事象は6です。したがって、

P(1の目が出る)＝P(2の目が出る)=P(3の目が出る)=P(4の目が出る)=P(5の目が出る)=P(6の目が出る)

と計算できます。

例題1：

さいころを1回投げて、奇数の目が出る確率はいくらでしょうか。

さいころを1回投げて奇数の目が出るのは、6つの目のうち、「1、3、5」の3つの目のいずれかが出る場合です。次のように計算できます。

例題2：

1～100の数字が1つだけ書かれた100枚のカードがあります。このカードから1枚を抜き取って、1~10までの数字が書かれたカードが出てくる確率はいくらでしょうか。

この問題では、根元事象は100個あります。また、1～10までのカードを引く事象は10通りあるので、次のように計算できます。