- Step1. 基礎編
- 9. 確率と期待値
9-6. 加法定理
■2つの事象が互いに排反である場合
事象Aと事象Bが互いに排反(同時に起こらない事象)である場合、次の式が成り立ちます。
この式を「加法定理」といいます。
例題1:
サイコロを1回投げます。このとき、「1」もしくは「2」が出る確率はいくらでしょうか。

サイコロを投げて「1」が出る確率を![]() 、「2」が出る確率を
、「2」が出る確率を![]() とします。「1」が出る確率は
とします。「1」が出る確率は![]() です。同様に、「2」が出る確率も
です。同様に、「2」が出る確率も![]() です。これらの2つの事象は同時には起こらないので、求める確率は加法定理により2つの和事象の確率になります。したがって、
です。これらの2つの事象は同時には起こらないので、求める確率は加法定理により2つの和事象の確率になります。したがって、
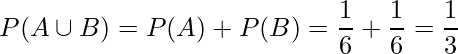
と算出できます。
■2つの事象が互いに排反ではない場合
事象Aと事象Bが互いに排反ではない場合、次の式が成り立ちます。この式は加法定理の一般的な形であり、上で述べたP(A∪B)=P(A)+P(B)はP(A∩B)=0のときのみ成り立つ式です。
この式は8-2章で学んだベン図を考えると分かりやすくなります。
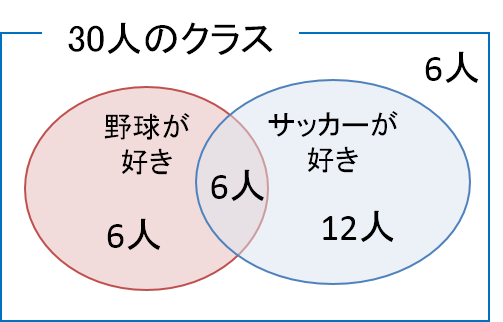
例えば事象Aを「野球が好き」、事象Bを「サッカーが好き」とします。図より野球が好きと答えたのは12人なので![]() 、サッカーが好きと答えたのは18人なので
、サッカーが好きと答えたのは18人なので![]() となります。
となります。
ただし、![]() を計算するために
を計算するために![]() と
と![]() をそのまま足してしまうと、「野球もサッカーが好き」と答えた6人が重複して含まれてしまいます。
をそのまま足してしまうと、「野球もサッカーが好き」と答えた6人が重複して含まれてしまいます。
そのため![]() から
から![]() を引く必要があります。
を引く必要があります。
したがって、ある人が「野球もしくはサッカーが好き」と答える確率は
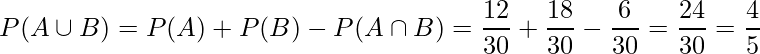
となります。
例題2:
1から30までの自然数の中からランダムに1つ数字を選んだ時、その数字が2もしくは3で割りきれる確率はいくらでしょうか。
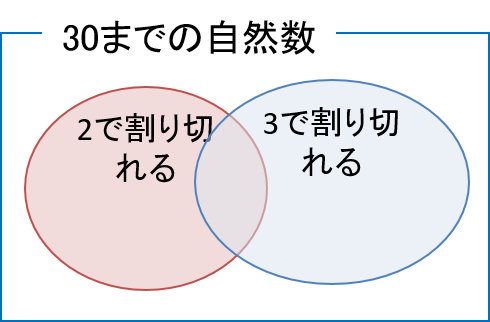
30までの自然数の中で、2で割り切れるものは15個(30/2=15)、3で割り切れるものは10個(30/3=10)あります。これらの数字の中にはそれぞれ6で割り切れる(=2でも3でも割り切れる)ものが5個(30/6=5)ずつ含まれています。
事象Aを「2で割り切れる」、事象Bを「3で割り切れる」とすると、加法定理より求める確率は
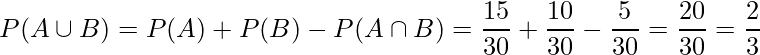
となります。
例題3:
1から50までの自然数の中からランダムに1つ数字を選んだ時、その数字が2もしくは3もしくは5で割りきれる確率はいくらでしょうか。
3つの事象がある場合には、加法定理により次の式が成り立ちます。
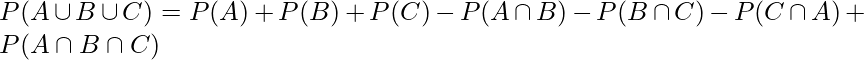
まずはじめに3つの事象それぞれの確率の和を求めます[P(A)+P(B)+P(C)]。この中にはAとB、BとC、CとAで重複しているものが含まれているのでこれらを引きます[-P(A∩B)-P(B∩C)-P(C∩A)]。ただし、AとBとCで重複しているものはP(A)+P(B)+P(C)の計算で3回分足し合わされており、-P(A∪B)-P(B∪C)-P(C∪A)の計算で3回分引かれてしまっています。そのため最後にP(A∩B∩C)を足します。
50までの自然数の中で、2で割り切れるものは25個(50/2=25)、3で割り切れるものは16個(50/3=16)、5で割り切れるものは10個(50/5=10)あります。これらの数字の中にはそれぞれ30で割り切れる(=2でも3でも5でも割り切れる)ものが1個(50/30=1)ずつ含まれています。
また、2と3で割り切れるものは8個(50/6=8)、3と5で割り切れるものは3個(50/15=3)、5と2で割り切れるものは5個(50/10=5)あります。
したがって、事象Aを「2で割り切れる」、事象Bを「3で割り切れる」、事象Cを「5で割り切れる」とすると、加法定理より求める確率は
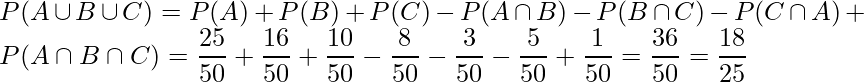
となります。






