- 9. 確率と期待値
練習問題(9. 確率と期待値)
1
ジョーカーを抜いた52枚のトランプから1枚をランダムに取り出すとき、ハートのエースが出る確率を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
ランダムに取り出すとき、どのカードが出るかは同様に確からしくなります。
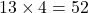 通りの取り出し方に対して、ハートのエースが出る事象は1通りしかありません。したがって、答えは
通りの取り出し方に対して、ハートのエースが出る事象は1通りしかありません。したがって、答えは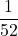 になります。
になります。
2
エースからキングまでのスペードのマークのトランプ13枚がある。この中からランダムに1枚取り出すとき、偶数のカードが出る確率を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
ランダムに1枚のカードを取り出すとき、取り出し方は全部で13通りあります。偶数のカードは{2, 4, 6, 8, 10, 12}の6枚あるので、求める確率は
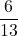 となります。
となります。
3
エースからキングまでのスペードのマークのトランプ13枚がある。この中からランダムに2枚取り出すとき、取り出したカードが2枚とも5以下となる確率を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
ランダムに2枚のカードを取り出すとき、取り出し方は全部で
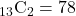 通りあります。5以下のカード2枚を取り出す組み合わせは
通りあります。5以下のカード2枚を取り出す組み合わせは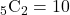 通りあります。以上から、求める確率は
通りあります。以上から、求める確率は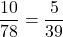 となります。
となります。
4
さいころを2回投げたとき、目の和が3以上になる確率を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
一見面倒臭そうに見えますが、さいころの目の和が3未満となる確率の余事象を考えると簡単です。さいころの2つの目の和が3未満、すなわち2以下となるのは、2つの目が1である事象1つしかありません。従って、1から「2回とも1が出る確率」を引いたものが求める確率となります。
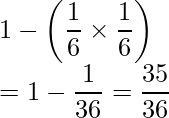
5
さいころを投げ、出た目の数の2乗個のアメをもらえるゲームをする。このゲームを1回やる時にもらえるアメの個数の期待値を求めよ。
例:5の目が出ると、5×5=25個のアメがもらえる。

答えを見る
- 答え
 閉じる
閉じる -
さいころのどの目が出る確率も
 であるので、期待値は次のように計算できます。
であるので、期待値は次のように計算できます。
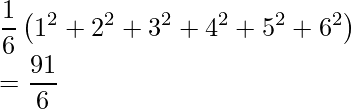
したがって、もらえるアメの個数の期待値は
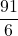 となります。
となります。







