ある事象が起こるという条件のもとで、別のある事象が起こる確率のことを「条件付き確率」と言います。例えば、事象Bが起こるという条件のもとで事象Aが起こる場合、この条件付き確率はと表され、次の式により計算できます。

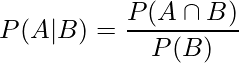
例題1：

次の図の袋の中には、赤い玉が3つ、白い玉が3つ入っています。赤い玉のうち2つには「1」、残りの1つには「2」と書かれています。一方、白い玉のうち2つには「2」、残りの1つには「1」と書かれています。この袋の中から玉を1つ取り出す時、「1」と書かれた赤色の玉が取り出される確率はいくらでしょうか。

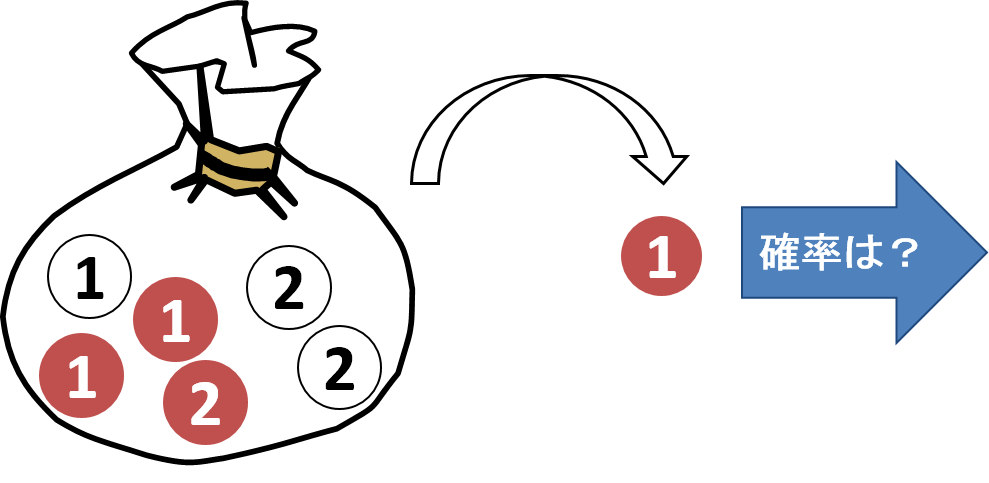
6個の玉の中に「1」と書かれた赤色の玉は2個あるので、となります。

例題2：

例題1と同じ袋の中から玉を1つ取り出した時、その玉は赤色でした。この赤い玉に「1」と書かれている確率はいくらでしょうか。

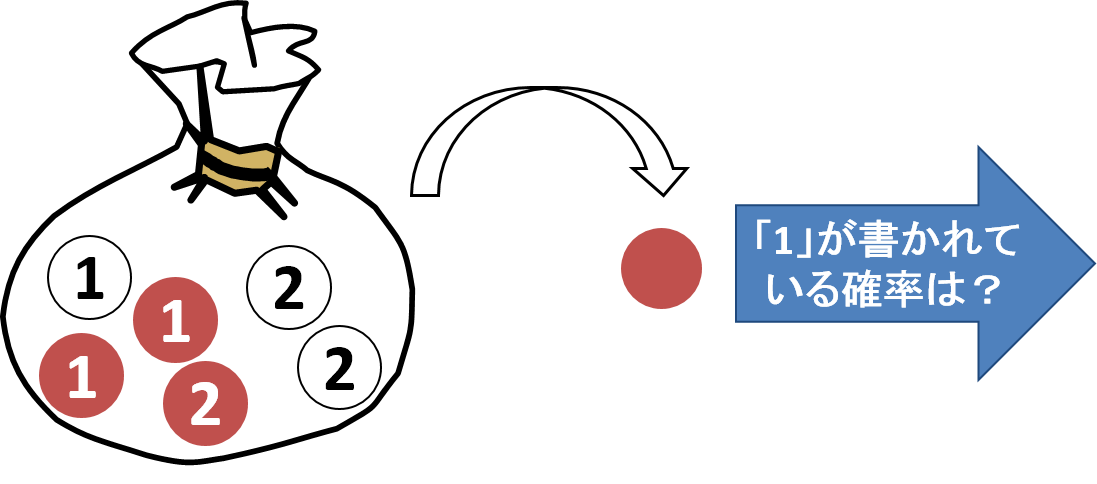
この問題は例題1と同じように、「玉は全部で6個、赤い玉で「1」と書かれた玉は2個あるから、と考えることはできません。なぜなら、既に玉の色は赤と分かっているので、このことを考慮する必要があるからです。このような場合の確率を「条件付き確率」といいます。

条件付き確率の式にあてはめて計算してみます。

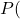• 赤玉である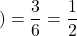　　（赤玉は全6個中3個含まれている）
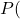• 1と書いて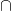ある赤玉である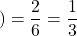　（「1」と書いてある赤玉は全6個中2個含まれている）

したがって、赤玉が取り出された場合に「1」と書いてある確率は次のように算出できます。

この結果は、3個の赤色の玉のうち「1」と書かれた玉は2個あるので、「1」が取り出される確率はであることを意味します。

例題3：

さいころを2回投げて出た目の和が8以上となる確率はいくらでしょうか。ただし、1回目に出た目は「4」であることが分かっています。

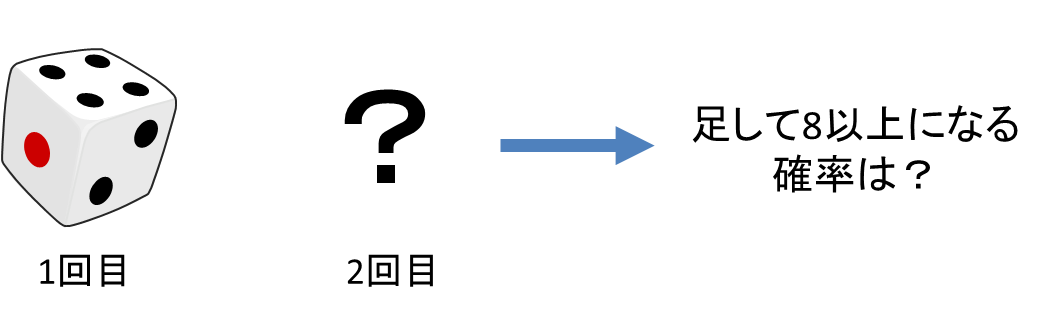
この問題では2回の試行による2つの結果から条件付き確率を求めます。

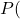• 1回目に出た目が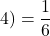
• 2回の目の和が8以上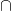1回目に出た目が4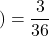（「サイコロを2回振った時の目の和が8以上、かつ1回目に出た目が4」となる目の組み合わせは（4, 4）（4, 5）（4, 6）の3通りあり、サイコロを2回振る場合に出る目の組み合わせは全部で36通りある）

したがって条件付き確率の式に当てはめると、求める条件付き確率は次のように算出できます。

■おすすめ書籍

ベイズ統計学をのイメージを掴むのには最適でした。一番分かりやすかったです。