- Step1. 基礎編
- 10. 条件付き確率とベイズの定理
10-2. 条件付き確率と独立
次のような袋の中から赤い玉が1つ取り出された時、この赤い玉に「1」と書かれている確率は、条件付き確率の式から![]() となります(10−2章 例題2再掲)。
となります(10−2章 例題2再掲)。
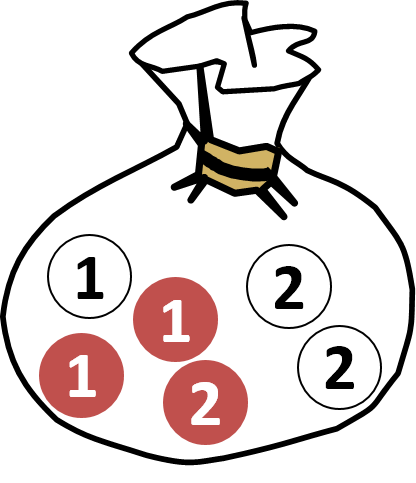

例題1:
この袋にさらに「1」と書かれた白い玉3個を加えます。この袋の中から玉を1つ取り出した時、その玉は赤色でした。この赤い玉に「1」と書かれている確率はいくらでしょうか。
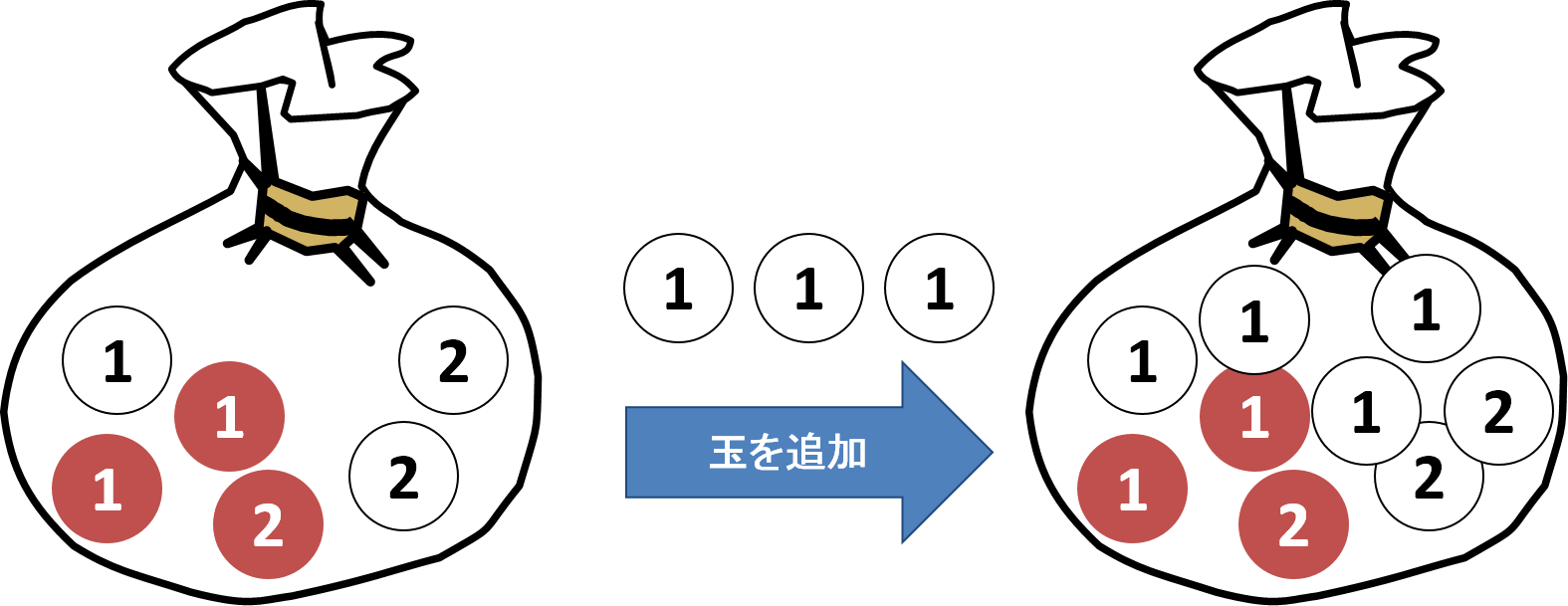
取り出された玉の色が赤である事象をB、玉に書かれている数字が「1」である事象をAとするとき、「取り出された玉の色が赤色で、その玉に書かれた数字が「1」であるという条件付き確率」は次のように計算されます。

一方、この袋の中には「1」と書かれた玉は6個あることから、取り出した玉の色を考慮しない場合、取り出した玉に書かれている数字が「1」となる確率は次のようになります。

つまり、取り出した玉が赤という情報があっても無くても、「1」と書かれた玉が取り出される確率は![]() となります。このように、事象Aの起こる確率が事象Bの影響を受けないとき、すなわち次の式が成り立つとき、事象Aと事象Bは「独立である」といいます。
となります。このように、事象Aの起こる確率が事象Bの影響を受けないとき、すなわち次の式が成り立つとき、事象Aと事象Bは「独立である」といいます。
【コラム】独立と排反のちがい
独立と混同しやすいものに「排反」があります。排反とは「事象Aと事象Bが互いに排反ならば、事象Bが起こったときに事象Aは起こらない」ということを意味します。条件付き確率の式を用いて表すと次のようになります。
10. 条件付き確率とベイズの定理
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 9. 確率と期待値
9-5. 確率と独立
- 10. 条件付き確率とベイズの定理
10-1. 条件付き確率とは






