確率において「独立」というのは非常に重要な概念です 。例えば、ここにコイン1枚とさいころ1個があるとします。コイン投げで表が出たときに、さいころの1の目が出やすくなったり出にくくなったりすることはありません。コイン投げの結果にかかわらず、さいころのどの目が出る確率もであるはずです。このように、お互いの結果が影響しあうことがないとき、2つの事象は「独立である」と言います。

2つの事象が独立である場合、2つの積事象の確率は事象同士の確率の積で算出することができます。つまり、独立な事象A、事象Bを同時に満たす事象（＝積事象）の確率について次のような関係が成り立ちます。

例題1：

コインの裏表とさいころの出る目が独立であるとき、両方を同時に投げて、コインが表でさいころの目が1となる確率はいくらになるでしょうか。

■数え上げる方法

コイン投げには表と裏の2通りがあり、さいころの出る目は6通りあります。したがって、合計での事象があることになります。このうち、コインが「表」でさいころの目が「1」である事象は1通りしかないので、となります。

■独立の性質を用いる方法

コインが表となる事象を事象A、さいころの出る目が1となる事象を事象Bとします。求める確率はです。それぞれの事象の確率は次のようになります。

• P(コインが表)=P(A)=

• P(さいころの出る目が1)=P(B)=

「さいころを投げる」試行に対して、「コインを投げる」試行は何の影響も与えない（コインの裏表によってさいころの出る目の確率は変わらない）ので、これらは独立であると言えます。したがって、 を使って次のように計算できます。

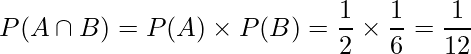
例題2：

さいころを2回投げて、6の目が2回連続で出る確率はいくらになるでしょうか。

1回目に6の目が出る事象を事象A、2回めに6の目が出る事象を事象Bとします。さいころを投げる試行において、1回目に6の目が出たからと言って、2回目は6の目が出やすくなったり出にくくなったりすることはなく、これらは独立な試行です。したがってを使うと、次のように計算できます。

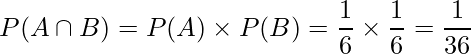
【コラム】確率における「独立」の重要性

積事象の確率を求める場合、事象同士が独立でない場合は、単純に掛け算による計算はできません。

例えば、例題1の「コインとさいころと両方を同時に投げて、コインが表でさいころの目が1となる確率はいくらになるでしょうか」という問題に、「ただし、コインが表だった場合、2の目がその他の目より2倍出やすくなる超常現象が起こる」というような条件が追加された場合は、両事象が独立ではないため単純に掛け算によって積事象の確率を算出することはできません。