- Step1. 基礎編
- 9. 確率と期待値
9-7. 期待値
期待値とは、1回の試行で得られる値の平均値のことで、得られうるすべての値とそれが起こる確率の積を足し合わせたものです。例えば次の表に示すように、n通りの結果![]() があり、それぞれの起こる確率が
があり、それぞれの起こる確率が![]() であるとします。
であるとします。
| 結果 | ・・・ | ||||
| 確率 | ・・・ |
このとき、期待値は次の式から計算できます。
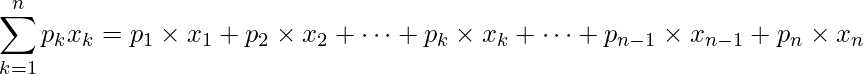
例題1:
さいころを1回投げるとき、出る目の期待値はいくらになるでしょうか。

| 出る目(x) | 1 | 2 | 3 | 4 | 5 | 6 |
| 確率(p) |
この期待値は、次のように計算します。
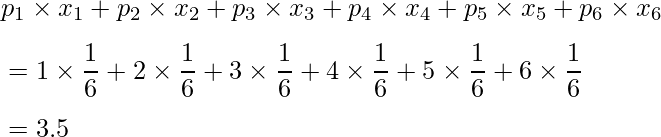
したがって、さいころを何回か投げると1回当たりの出る目の平均は3.5になると期待できます。
例題2:
さいころを投げて、出た目の数×100円貰えるゲームをします。このゲームを1回やるとき、いくら貰えると考えられるでしょうか。

| 出る目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 貰える金額(x) | 100円 | 200円 | 300円 | 400円 | 500円 | 600円 |
| 確率(p) |
どの目が出る確率も![]() で、金額は100円から600円まで変わります。このゲームで貰える金額の期待値は、次のように計算できます。
で、金額は100円から600円まで変わります。このゲームで貰える金額の期待値は、次のように計算できます。
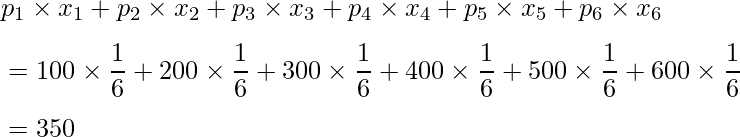
この結果から、「このゲームを1回行うごとに350円くらいもらえると見込んでよい(期待できる)」ということが分かりました。しかしこれは「1回やれば確実に350円もらえる」という意味ではないことに注意してください。
例題3:
コインを1枚投げたときに、表が出たら100円がもらえるが、裏が出たら100円を支払わなくてはならないゲームをします。このゲームを1回やるとき、いくら貰えると考えられるでしょうか。

| コイン | 表 | 裏 |
| 貰える金額(x) | 100円 | -100円 |
| 確率(p) |
この期待値は、
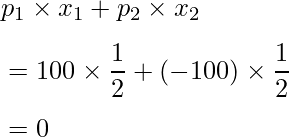
となり、このゲームでは何ももらえない(=儲けがなさそう)ということが期待できます。
9. 確率と期待値
事前に読むと理解が深まる- 学習内容が難しかった方に -
- ブログ
平均寿命






