- Step1. 基礎編
- 10. 条件付き確率とベイズの定理
10-4. ベイズの定理
いくつかの袋の中に赤い玉と白い玉がいくつか入っています。これらの袋のうちどれか1つの袋から、いくつかの玉を取り出したとします。この取り出された玉の色(結果)から、どの袋から取り出されたものか(原因)を推定することを考えます。ここで用いるのが「ベイズの定理」です。
事象Aが起こるという条件のもとで、k種類の事象![]() :ただしこれらは互いに排反とする
:ただしこれらは互いに排反とする![]() が起こるとします。このとき、事象Aが起こるという条件のもとで、事象
が起こるとします。このとき、事象Aが起こるという条件のもとで、事象![]() が起こる条件付き確率
が起こる条件付き確率![]() は次の式から求められます。
は次の式から求められます。
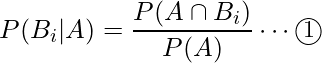
ここで乗法定理![]() を①に代入します。これがベイズの定理です。
を①に代入します。これがベイズの定理です。
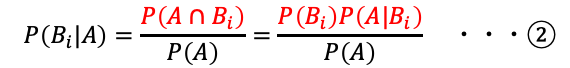
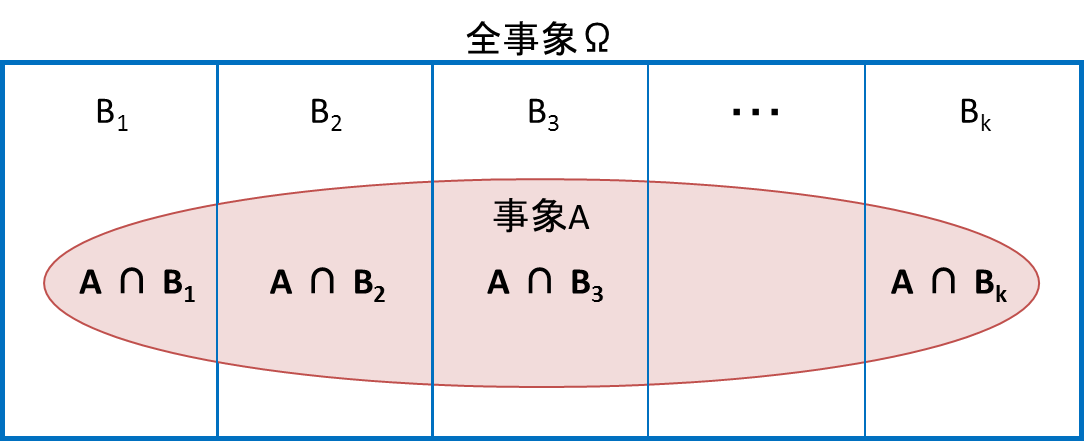
P(A)は![]() と書けます。これは、次の図のそれぞれの事象
と書けます。これは、次の図のそれぞれの事象![]() における赤い事象Aの部分を足し合わせたものだと考えることができます。この式を②に代入します。
における赤い事象Aの部分を足し合わせたものだと考えることができます。この式を②に代入します。
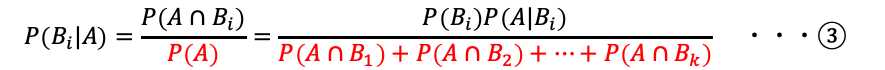
③にも乗法定理![]() を適用すると、次の式が導かれます。
を適用すると、次の式が導かれます。
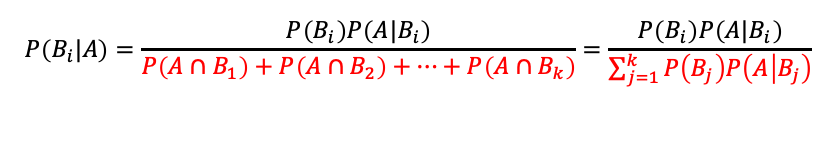
例題:
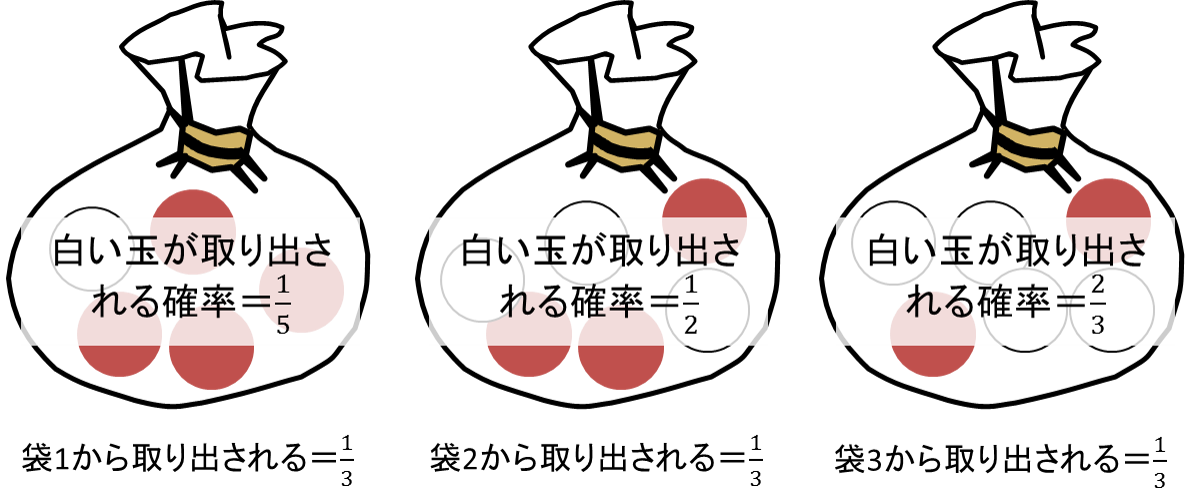
3つの袋があり、次のように赤い玉と白い玉が入っています。
- 袋1:赤い玉4つ、白い玉1つ
- 袋2:赤い玉3つ、白い玉3つ
- 袋3:赤い玉2つ、白い玉4つ
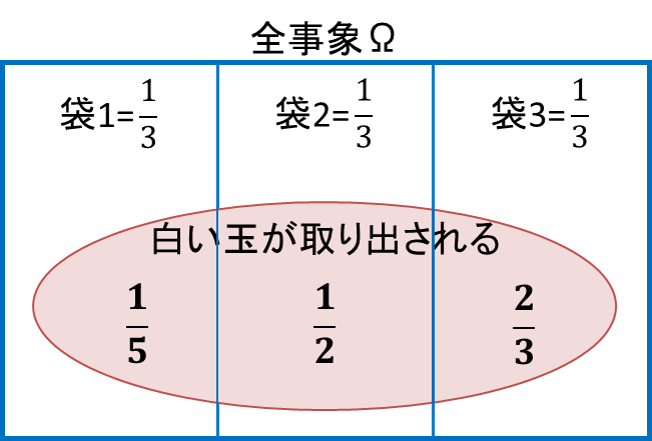
いずれかの袋から玉を1つ取り出したところ、白い玉でした。この玉が袋2から取り出された確率はいくらでしょうか。
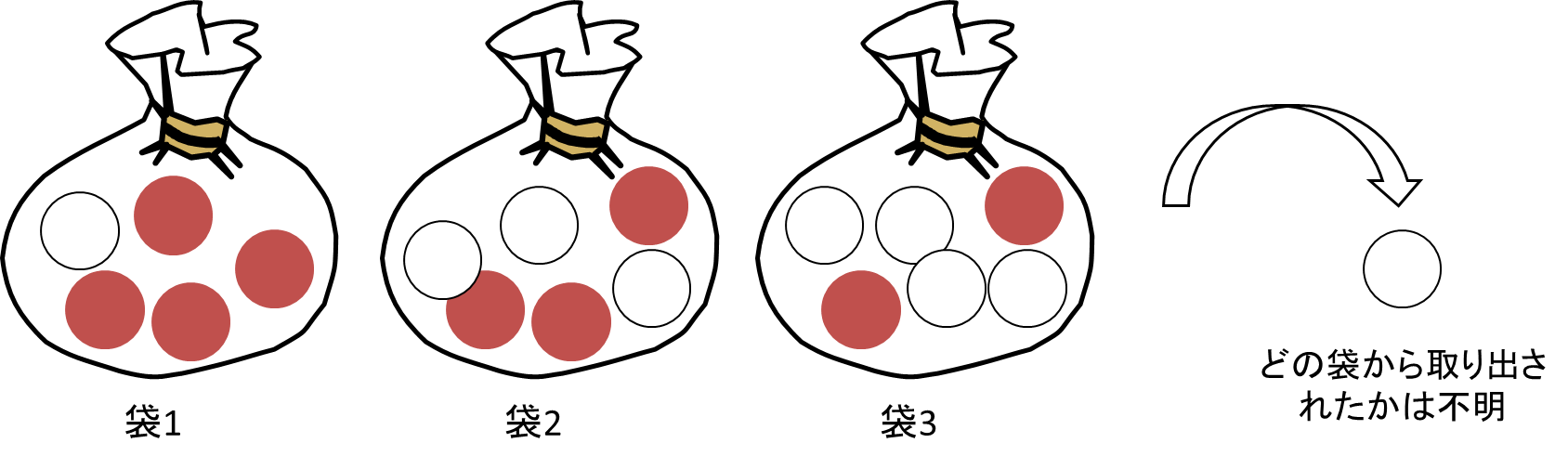
白い玉が取り出されたという事象を事象A、玉を袋1から取り出す事象を事象![]() 、袋2から取り出す事象を事象
、袋2から取り出す事象を事象![]() 、袋3から取り出す事象を事象
、袋3から取り出す事象を事象![]() をとします。袋は3つあり、これらの袋のどれか1つが選ばれる確率は全て等しいと考えられるので、次のようになります。
をとします。袋は3つあり、これらの袋のどれか1つが選ばれる確率は全て等しいと考えられるので、次のようになります。
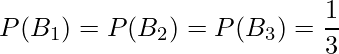
また、白い玉が取り出される確率は次のようになります。
袋1の場合:
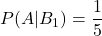
袋2の場合:
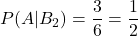
袋3の場合:
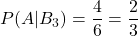
したがってベイズの定理の式に当てはめると、
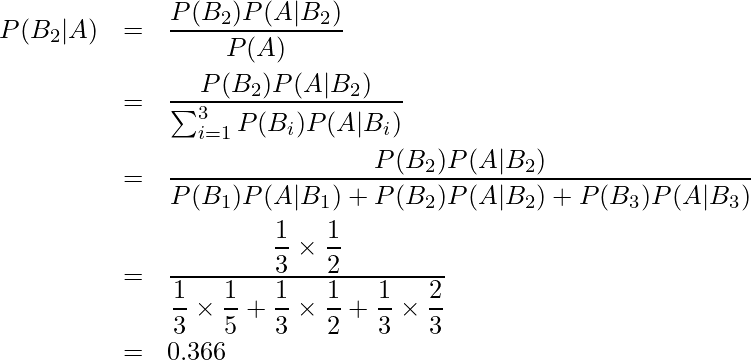
となり、いずれかの袋から取り出した玉が白い玉だったときに、それが袋2から取り出された確率は0.366となります。
■おすすめ書籍
こちらは、会話形式で進んでいきますが、内容はとてもボリューミーです。
10. 条件付き確率とベイズの定理
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 9. 確率と期待値
9-5. 確率と独立
- 10. 条件付き確率とベイズの定理
10-1. 条件付き確率とは
- 10. 条件付き確率とベイズの定理
10-3. 乗法定理
- ブログ
病気である確率








