- Step1. 基礎編
- 10. 条件付き確率とベイズの定理
10-6. ベイズの定理の使い方
例題:
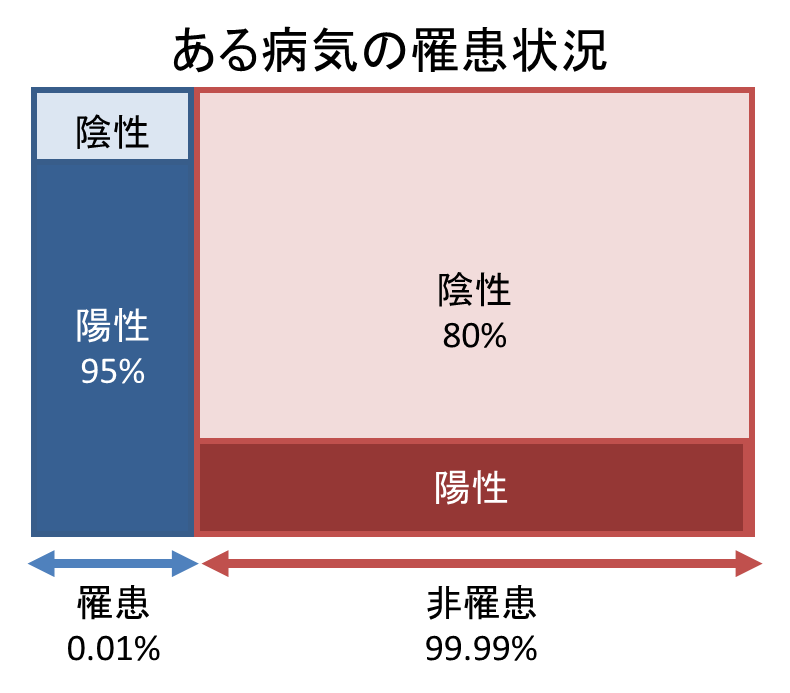
日本人の0.01%が罹患しているある病気について考えます。この病気の検査方法では、実際に病気に罹患している人が陽性と判定される確率が95%、逆に罹患していない人が陰性と判定される確率は80%であると言われています。 ある人がこの病気の検査を受けて陽性という判定を受けた時、本当にこの病気に罹患している確率はいくらでしょうか。
検査で陽性になる事象を事象![]() 、検査で陰性になる事象を事象
、検査で陰性になる事象を事象![]() (事象Aの余事象)、実際に病気に罹患している事象を事象
(事象Aの余事象)、実際に病気に罹患している事象を事象![]() 、罹患していない事象を事象
、罹患していない事象を事象![]() とします。ベイズの定理を使うと、求める確率は
とします。ベイズの定理を使うと、求める確率は![]() となります。
となります。
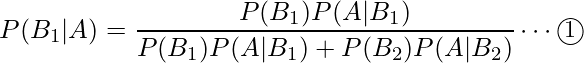
問題文から、それぞれの確率は次のようになります。
- 病気に罹患している確率:
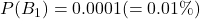
- 病気に罹患していない確率:
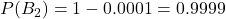
- 実際に罹患している人が検査で陽性となる確率:
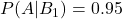
- 実際に罹患していない人が検査で陰性となる確率:
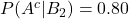
- 実際に罹患していない人が検査で陽性となる確率:
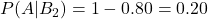
これらの値を①の式に当てはめると、
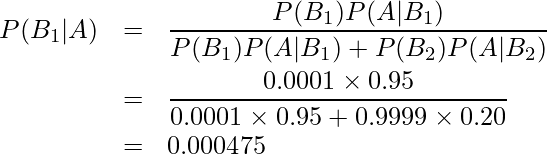
となり、陽性と判定されたときに実際に病気に罹患している確率は0.0475%であることが分かります。したがってこの検査法の場合、陽性という判定を受けてもあまり気を病む必要はないかもしれません。
医学におけるこのような検査では、次のような用語が用いられます。
10. 条件付き確率とベイズの定理
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 統計Tips
2行×2列のクロス集計表の統計量
- 統計解析事例
ROC曲線
- 10. 条件付き確率とベイズの定理
10-4. ベイズの定理
- ブログ
病気である確率






