- 10. 条件付き確率とベイズの定理
練習問題(10. 条件付き確率とベイズの定理)
1
1から3の目が赤色で塗られており、4から6の目は青色で塗られているさいころがある。今、このさいころを投げて青色の目が出た時、この目が偶数である確率を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
青色の目が出る事象をA、偶数の目が出る事象をBとすると、求める確率は
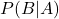 となります。
となります。 となる事象は出る目が{4, 6}の場合なので、
となる事象は出る目が{4, 6}の場合なので、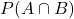 は次のようになります。
は次のようになります。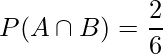
以上から、次のように確率が求められます。
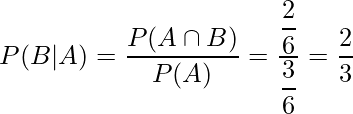
2
表と裏の面が赤か青で塗られている3枚のカードA, B, Cがあり、それぞれのカードの面の色は次のようになっている。
- カードA:両面とも青色で塗られている
- カードB:片面が赤色、もう片面が青色で塗られている
- カードC:両面とも赤色で塗られている。
このカード3枚を袋に入れてよく混ぜて、目をつぶったまま1枚を取り出し、机の上に置いて目を開けるとカードは赤色だった。このとき、ひっくり返した面も赤色である確率を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
目を開けて見えた面のカードが赤色である事象をA、ひっくり返した面が赤色である事象をBとします。求める確率は
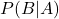 と表すことができるので、この条件付き確率を求めればよいことが分かります。
と表すことができるので、この条件付き確率を求めればよいことが分かります。まず
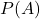 について考えます。
について考えます。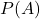 は、次の場合が考えられます。
は、次の場合が考えられます。- カードBの赤い面が見えるように引く場合
- カードCの赤い面が見えるように引く場合
これは
 となります。(カードBが選ばれ、更に赤い面が上となる確率)
となります。(カードBが選ばれ、更に赤い面が上となる確率)これは
 となります。(カードCが選ばれる確率)
となります。(カードCが選ばれる確率)以上から、
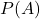 は次のようになります。
は次のようになります。
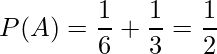
次に、
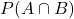 について考えます。これは、「赤い面が見えるようにカードを引き、さらにひっくり返した面も赤色である確率」のことです。つまりカードCを引けばよいことが分かります。
カードCは両面とも赤色であるため、どちらの面が出るかは考える必要がありません。よって、
について考えます。これは、「赤い面が見えるようにカードを引き、さらにひっくり返した面も赤色である確率」のことです。つまりカードCを引けばよいことが分かります。
カードCは両面とも赤色であるため、どちらの面が出るかは考える必要がありません。よって、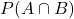 は次のようになります。
は次のようになります。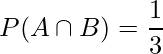
以上のことから、
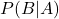 は次のように求められます。
は次のように求められます。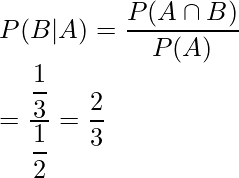
3
一郎、二郎、三郎、四郎の4人がボウリングでストライクを出す確率は50%, 70%, 90%, 98%である。4人のうち1人が球を投げてストライクを出したときに、それが一郎である確率はいくらか。

答えを見る
- 答え
 閉じる
閉じる -
ストライクを出したという事象を事象A、一郎が球を投げる事象を事象
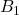 、二郎が球を投げる事象を事象
、二郎が球を投げる事象を事象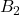 、三郎が球を投げる事象を事象を事象
、三郎が球を投げる事象を事象を事象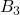 、四郎が球を投げる事象を事象を事象
、四郎が球を投げる事象を事象を事象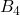 をとします。4人から1人が選ばれる確率は全て等しいと考えられるので、次のようになります。
をとします。4人から1人が選ばれる確率は全て等しいと考えられるので、次のようになります。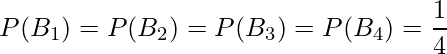
したがってベイズの定理の式に当てはめると、
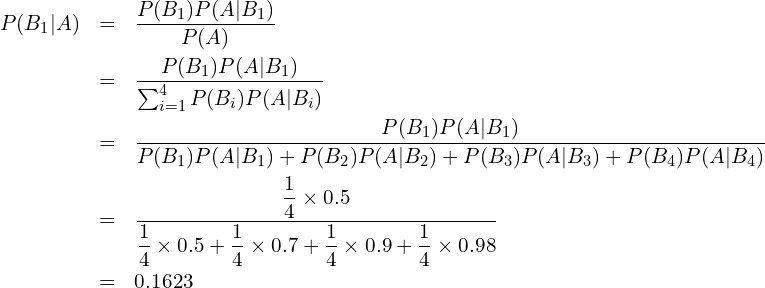
よって答えは16.23%となります。一郎はまだまだボウリングの練習が必要そうです。
4
ある映画の試写会を行い、満足度のアンケート調査を行った。試写会に参加したのは300人でそのうち女性が180人であり、満足したと回答したのは男性の50%、女性の75%であった。この映画を見て満足しなかったと答えた人が女性である確率はいくらか。

答えを見る
- 答え
 閉じる
閉じる -
映画に満足しなかった事象を事象A、アンケートに答えたのが男性である事象を事象
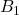 、アンケートに答えたのが女性である事象を事象
、アンケートに答えたのが女性である事象を事象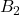 とします。
とします。計算に必要な確率は次のように計算できます。
- アンケートに答えたのが男性である確率:
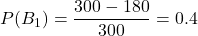
- アンケートに答えたのが女性である確率:
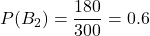
- 映画を見た男性が満足しない確率:
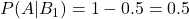
- 映画を見た女性が満足しない確率:
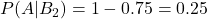
したがってベイズの定理の式に当てはめると、
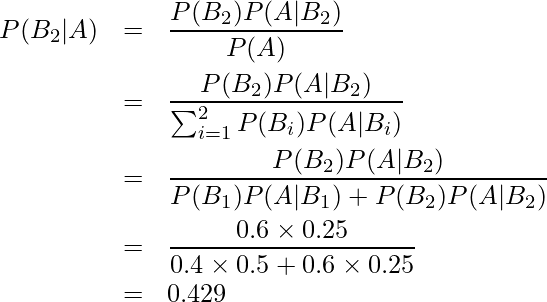
したがって、答えは42.9%となります。
- アンケートに答えたのが男性である確率:
5
人の「疲れ」を判定する機械が発明された。この機械に人が入ると「疲れている」か「疲れていない」かを判定してくれる画期的なものである。この機械を使うと、疲れている人の95%を「疲れている」と判定し、疲れていない人の98%を「疲れていない」と判定するということが分かっている。
人の70%は疲れているという研究結果があるとき、ある人がこの機械に入って「疲れている」と判定された場合に実際に疲れている確率はいくらか。(すべて架空の話です)

答えを見る
- 答え
 閉じる
閉じる -
検査で「疲れている」と判定される事象を事象
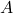 、検査で「疲れていない」と判定される事象を事象
、検査で「疲れていない」と判定される事象を事象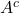 (事象Aの余事象)、実際に疲れている事象を事象
(事象Aの余事象)、実際に疲れている事象を事象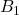 、疲れていない事象を事象
、疲れていない事象を事象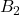 とします。ベイズの定理を使うと、求める確率は
とします。ベイズの定理を使うと、求める確率は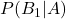 となります。
となります。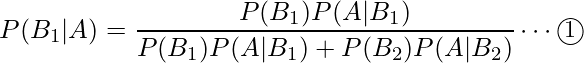
問題文から、それぞれの確率は次のようになります。
- 実際に疲れている確率:
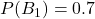
- 実際に疲れていない確率:
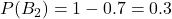
- 実際に疲れている人が機械で「疲れている」と判定される確率:
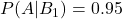
- 実際に疲れていない人が機械で「疲れていない」と判定される確率:
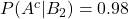
- 実際に疲れていない人が機械で「疲れている」と判定される確率:
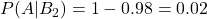
これらの値を①の式に当てはめると、
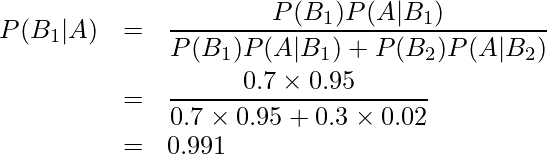
となり、「疲れている」と判定されたときに実際に疲れている確率は99.1%であることが分かります。驚くべき精度ですね!
- 実際に疲れている確率:







