- Step1. 基礎編
- 10. 条件付き確率とベイズの定理
10-3. 乗法定理
「事象Bが起こるという条件のもとで、事象Aが起こる条件付き確率![]() 」が下の式から求められることは10‐1章で既に学びました。
」が下の式から求められることは10‐1章で既に学びました。
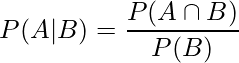
この条件付き確率の式の両辺に![]() をかけて次のように変形したものを「乗法定理」といいます。
をかけて次のように変形したものを「乗法定理」といいます。
あるいはAとBを入れ替えて、次のようにも書くことができます。
例題:
4本の当たりを含んだ10本のくじがあります。この中から太郎さんがくじを1本引き、そのくじを戻した後に花子さんがくじを引くとき、太郎さんも花子さんも当たりくじを引く確率はいくらでしょうか。
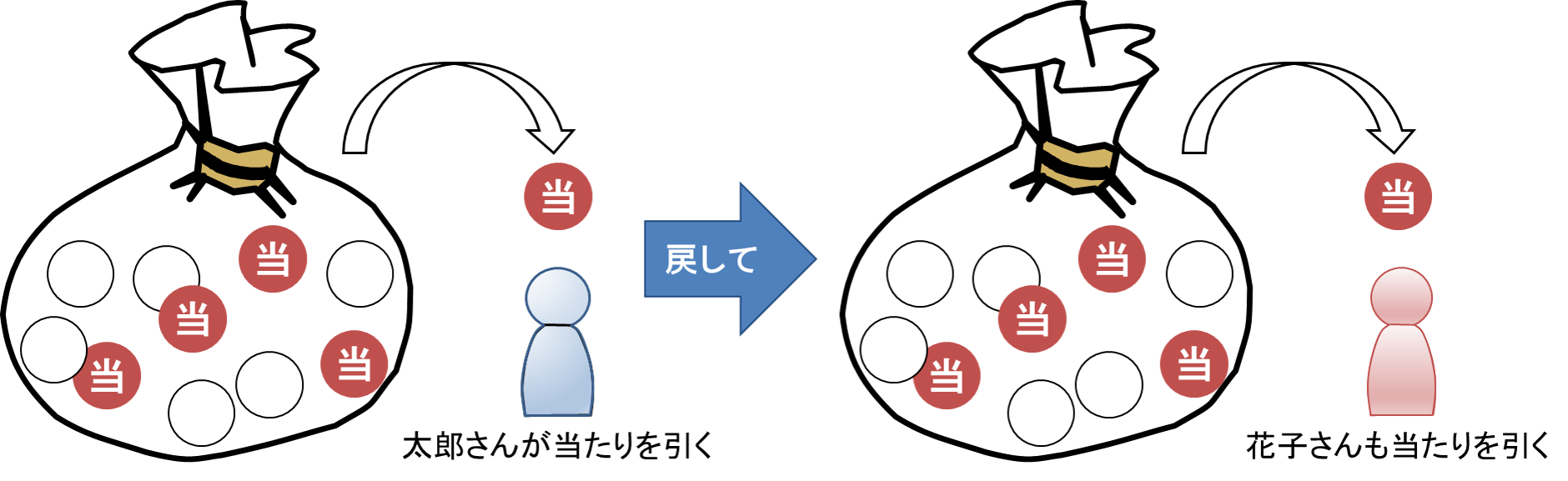
太郎さんがくじを引いた後に、そのくじを戻して花子さんがくじを引いているので、太郎さんの結果によって花子さんが当たりくじを引く確率は変化しません。したがって、太郎さんが当たりくじを引く事象と花子さんが当たりくじを引く事象は独立です。9-5章で学んだように、2つの事象が独立である場合、2つの積事象の確率は事象同士の確率の積で算出することができます。
太郎さんが当たりくじを引く確率を![]() 、花子さんが当たりくじを引く確率を
、花子さんが当たりくじを引く確率を![]() とおくと、
とおくと、
太郎さんが当たりくじを引く確率:
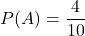 (10本中当たりは4本含まれている)
(10本中当たりは4本含まれている)花子さんが当たりくじを引く確率:
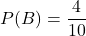 (10本中当たりは4本含まれている)
(10本中当たりは4本含まれている)
となることから、太郎さんも花子さんも当たりを引く確率は次のように算出できます。
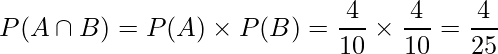
例題2:
4本の当たりを含んだ10本のくじがあります。この中から太郎さんがくじを1本引き、そのくじを戻さずにさらに花子さんがくじを引くとき、太郎さんも花子さんも当たりくじを引く確率はいくらでしょうか。
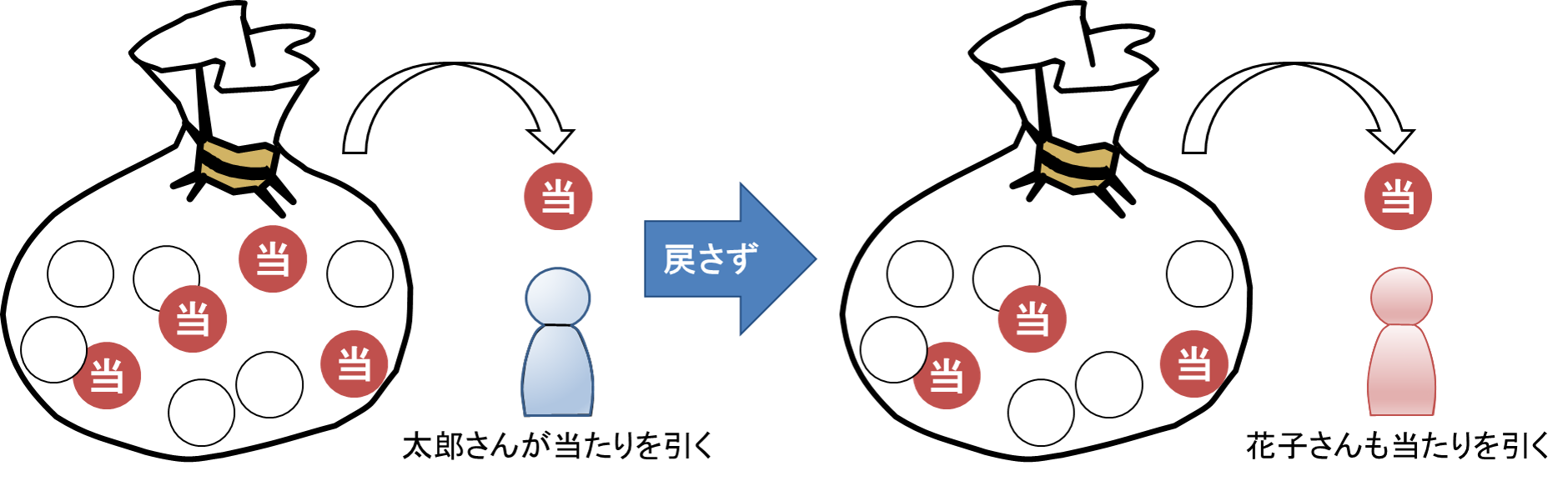
この問題では、例題1のように2つの事象は独立であると考えることはできません。なぜなら、太郎さんの結果によって花子さんが当たりくじを引く確率は変化するからです。このような問題のときには「乗法定理」を使います。太郎さんが当たりくじを引く確率を![]() 、花子さんが当たりくじを引く確率を
、花子さんが当たりくじを引く確率を![]() とおきます。
とおきます。
- 太郎さんが当たりくじを引く確率:
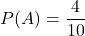 (10本中当たりは4本含まれている)
(10本中当たりは4本含まれている) - 太郎さんが当たりくじを引いた後で、それを戻さずに花子さんが当たりくじを引く確率:
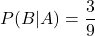 (残り9本中当たりは3本含まれている)
(残り9本中当たりは3本含まれている)
したがって、太郎さんも花子さんも当たりを引く確率は乗法定理を用いて次のように求められます。
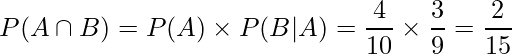
10. 条件付き確率とベイズの定理
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 9. 確率と期待値
9-5. 確率と独立
- 10. 条件付き確率とベイズの定理
10-1. 条件付き確率とは






