Step1. 基礎編
11. 確率変数と確率分布

11-2. 離散型確率分布と確率質量関数

確率変数には、「離散型」と「連続型」の2種類があります。この章では離散型確率変数について説明します。

■離散型確率変数

離散型変数はとびとびの値をとる変数のことで、隣り合う数字の間には値が存在しないものを指します。離散型変数には、さいころの出る目や人数などが含まれます。例えば、さいころの3の目の次は4であり、その間に3.2や3.5といった数値は存在しません。

次の表で示すように、離散型変数 $X$ の取りうる値（ $x_1, x_2, \cdots$ ）それぞれに対応する確率 $p$ が存在する場合、この変数を「離散型確率変数」といいます。

X	$x_1$	$x_2$	・・・	$x_{n-1}$	$x_n$
$P(X)$	$p_1$	$p_2$	・・・	$p_{n-1}$	$p_n$

■離散型確率分布

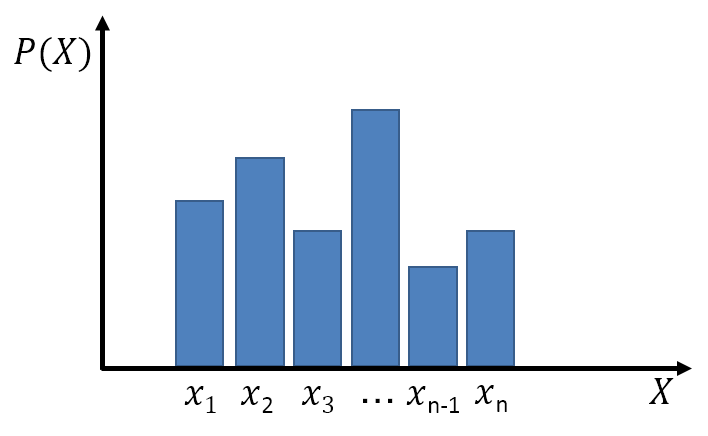
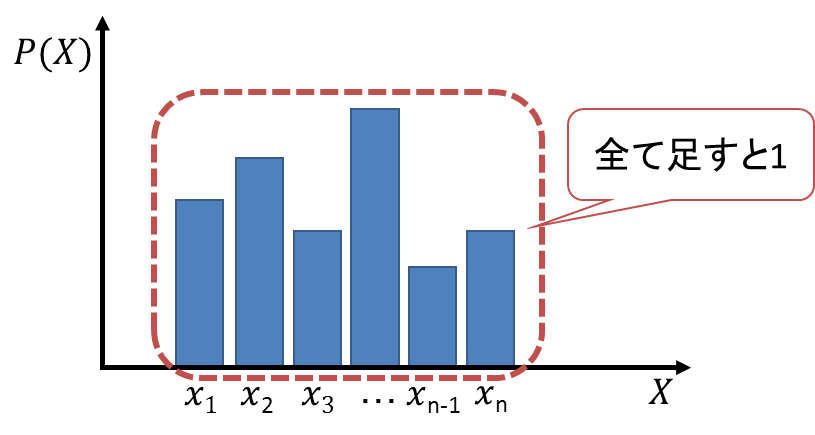
確率変数が離散型である場合の確率分布を「離散型確率分布」、あるいは「離散型分布」といいます。次の図は離散型確率分布のイメージを表したものです。横軸は確率変数 $X$ を、縦軸は $X$ の確率である $P(X)$ を表します。

■確率質量関数

離散型確率変数 $X$ がある値 $x$ をとる確率を関数 $f(x)$ とした場合、 $f(x)$ は「確率質量関数」と呼ばれます。 $f(x)$ を使うと、 $X=x$ （ある値 $x$ ）となる確率は次のように表すことができます。

$f(x)=P(X=x)$

確率の約束の1つとして、「全事象が起こる確率は1である」ことは9‐1章で既に学びました。このことは、離散型確率分布では次のように表すことができます。

$\displaystyle \sum_{i=1}^n P(X=x_i)= P(X=x_1) + P(X=x_2) + \cdots +P(X=x_n)=1$

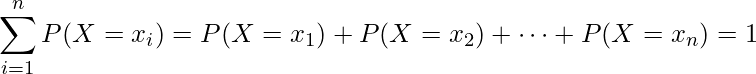
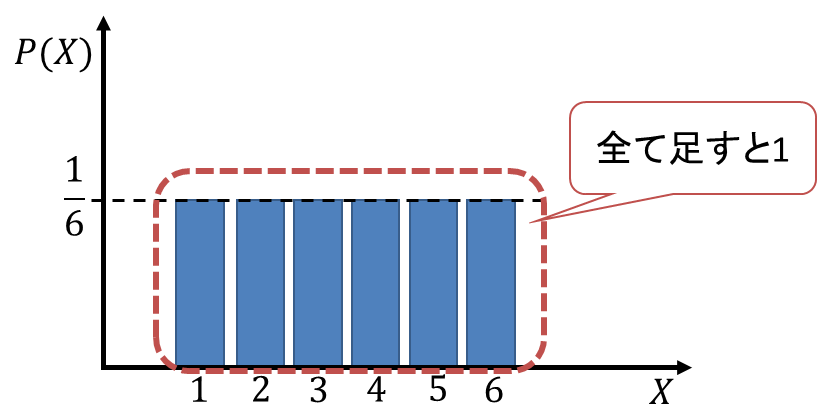
さいころを1回投げる場合を例にとります。確率変数 $X$ をさいころの出る目を $x_i \hspace{3mm}(i=1, 2, 3, 4, 5, 6)$ とすると、すべての $x_i$ について $P(X=x_i)\displaystyle = \frac{1}{6}$ であることから、これらの確率の総和は次のように「1」と計算できます。

$\vspace{3mm}\displaystyle \sum_{i=1}^6 P(X=x_i) \\ \vspace{3mm}= P(X=1) + P(X=2) + P(X=3)+P(X=4)+P(X=5)+P(X=6) \\ \vspace{3mm} = \displaystyle \frac{1}{6} +\displaystyle \frac{1}{6} +\displaystyle \frac{1}{6} +\displaystyle \frac{1}{6} +\displaystyle \frac{1}{6} +\displaystyle \frac{1}{6} \\ \vspace{3mm} = 1$