確率変数の期待値には、4つの重要な性質があります。これらの性質は、離散型確率変数、連続型確率変数いずれにおいても成立します。さいころを投げて出る目（＝確率変数）を例として、これらの性質について解説します。なお12-3章で計算したように、ここではであることを用います。またCは値の変化しない定数とします。

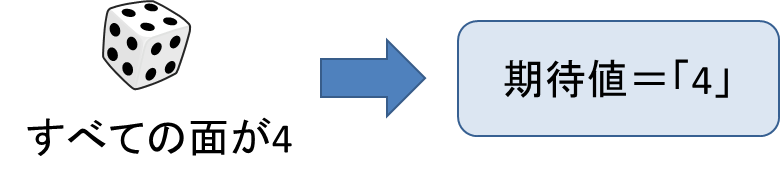
1. E(C)=C

定数の期待値は定数になります。

例：すべての目が4であるさいころを投げる場合、出る目の期待値は「4」になります。

2. E(X+C)=E(X)+E(C)=E(X)+C

確率変数に定数を足した場合の期待値は、元の確率変数の期待値に定数を足したものになります。

例：さいころを投げて出る目に3を足す場合の期待値は、元の確率変数の期待値であるに3を足した「6.5」になります。

3. E(kX)=kE(X)

確率変数を定数倍したものの期待値は、元の確率変数の期待値を定数倍したものになります。

例：さいころを投げて出る目を4倍する場合の期待値は、元の確率変数の期待値であるE(X)=3.5に4を掛けた「14」になります。

4. E(X+Y)=E(X)+E(Y)

確率変数の和の期待値は、それぞれの期待値の和に等しくなります。この性質は2つの確率変数が独立でなくても成り立ちます。

例：異なるさいころAとBを投げて両方の出る目を足す場合の期待値は、さいころAの期待値「3.5」とさいころBの期待値「3.5」の和である「7」になります。