- Step1. 基礎編
- 12. 累積分布関数と確率変数の期待値・分散
12-3. 確率変数の期待値
確率変数の期待値は、確率変数がとる値とその値をとる確率の積を全て足し合わせたもので、確率変数の平均値を表します。期待値は分布の特徴を掴むために用いられる情報の一つであり、Expectation(期待)の頭文字の「![]() 」を用いて表します。例えば、確率変数
」を用いて表します。例えば、確率変数![]() の期待値は「
の期待値は「![]() 」と表します。
」と表します。
■離散型確率変数の場合
離散型確率変数の期待値の場合の期待値は、確率変数![]() がとり得るそれぞれの値
がとり得るそれぞれの値![]() に対応する確率
に対応する確率![]() を掛け、掛けた結果を全て足し合わせることで算出できます。
を掛け、掛けた結果を全て足し合わせることで算出できます。
| ・・・ | |||||
| ・・・ |
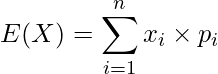
例えばさいころを投げて出る目を確率変数![]() とするとき、期待値は次のようになります。
とするとき、期待値は次のようになります。
| さいころの出る目 ( | 1 | 2 | 3 | 4 | 5 | 6 |
| 確率 ( |
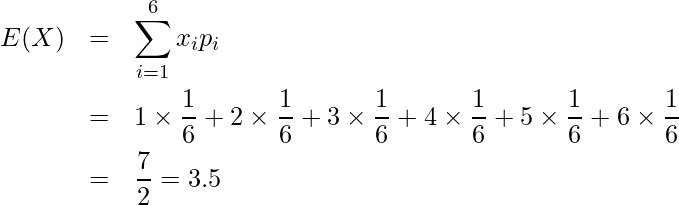

■連続型確率変数の場合
連続型確率変数の場合の期待値は、積分によって計算することができます。
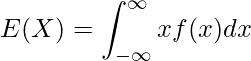
例えば確率密度関数![]() において、確率変数
において、確率変数![]() が0から6の範囲をとるとき
が0から6の範囲をとるとき![]() 、期待値は次のようになります。
、期待値は次のようになります。
![Rendered by QuickLaTeX.com \begin{eqnarray*} E(X)&=& \displaystyle \int_{0}^{6} xf(x)dx \\ &=&\displaystyle \int_{0}^{6} x \times \displaystyle \frac{1}{6} dx \\ &=&\left[ \displaystyle \frac{x^2}{12} \right]_0^6 \\ &=&3 \end{eqnarray*}](https://bellcurve.jp/statistics/wp-content/ql-cache/quicklatex.com-1240f0084dc60d178455634b80d91584_l3.png)
【コラム】確率変数の期待値?分布の期待値?
この章で求めた期待値![]() は、「確率変数
は、「確率変数![]() の分布の期待値」です。この
の分布の期待値」です。この![]() を、「分布の期待値」や「
を、「分布の期待値」や「![]() の期待値」「確率変数
の期待値」「確率変数![]() の期待値」といった言い方をすることがありますが、「確率変数
の期待値」といった言い方をすることがありますが、「確率変数![]() の分布の期待値」と同じものを指します。
の分布の期待値」と同じものを指します。
この後の章では二項分布や一様分布など、様々な分布を扱います。そのとき、「●●分布の期待値」という言葉が出てきますが、これは確率変数![]() が●●分布に従っている場合の「確率変数
が●●分布に従っている場合の「確率変数![]() の分布の期待値」を意味します。
の分布の期待値」を意味します。
12. 累積分布関数と確率変数の期待値・分散
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 9. 確率と期待値
9-6. 期待値
- 11. 確率変数と確率分布
11-2. 離散型確率分布と確率質量関数
- 11. 確率変数と確率分布
11-3. 連続型確率分布







