- Step1. 基礎編
- 15. いろいろな確率分布3
15-2. 離散一様分布
一様分布には「離散一様分布(離散型一様分布)」と「連続一様分布(連続型一様分布)」があります。この章では離散一様分布について説明します。離散一様分布は、確率変数![]() が離散型である場合に、すべての事象の起こる確率が等しい分布のことです。
が離散型である場合に、すべての事象の起こる確率が等しい分布のことです。

確率変数![]() が離散一様分布に従うとき、
が離散一様分布に従うとき、![]() となる確率
となる確率![]() は、
は、![]() を確率変数Xの取りうる個数とすると次のように計算されます。
を確率変数Xの取りうる個数とすると次のように計算されます。
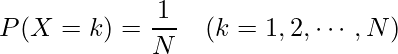
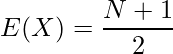
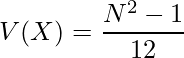
また、次のような場合には
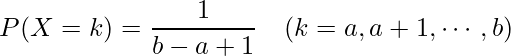
Xの期待値![]() と分散
と分散![]() は次のようになります。
は次のようになります。
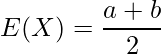
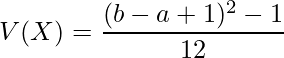
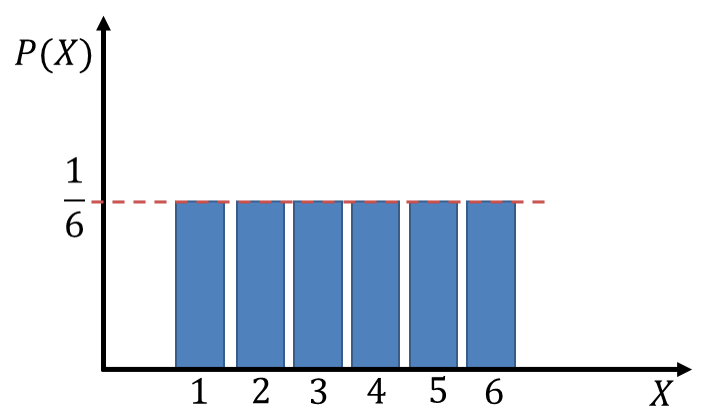
例えば、さいころの1から6までの目が出る確率は全て等しいことから、離散一様分布に従います。さいころの目は全部で6つなので![]() =6となります。したがって、さいころの出る目を
=6となります。したがって、さいころの出る目を![]() とすると、それぞれの目が出る確率は次のようになります。
とすると、それぞれの目が出る確率は次のようになります。
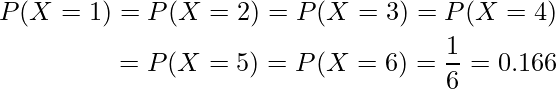

![]() の期待値と分散は次のように計算できます。
の期待値と分散は次のように計算できます。
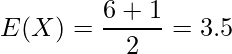
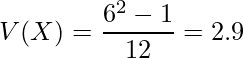
15. いろいろな確率分布3
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 9. 確率と期待値
9-6. 期待値
- 6. 分散と標準偏差
6-1. 分散
- 11. 確率変数と確率分布
11-2. 離散型確率分布と確率質量関数
- 12. 累積分布関数と確率変数の期待値・分散
12-3. 確率変数の期待値
- 12. 累積分布関数と確率変数の期待値・分散
12-5. 確率変数の分散






