- Step1. 基礎編
- 15. いろいろな確率分布3
15-4. 連続一様分布2
例題1:
0以上5以下の範囲で乱数を10,000個作成したとき、その中で1以上2以下の値をとる確率はいくらでしょうか。
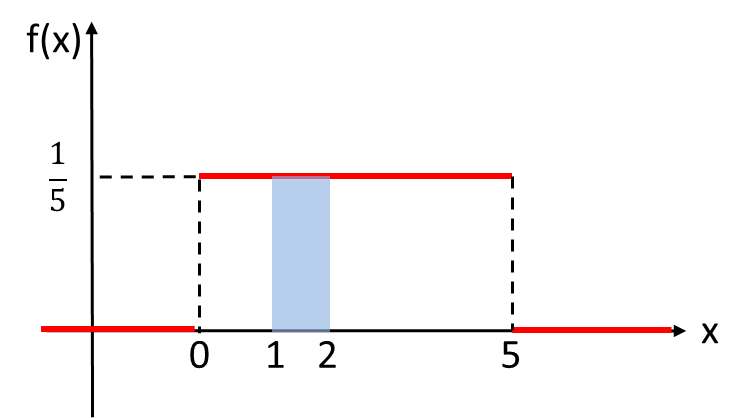
乱数を発生させているので、求める確率は一様分布を用いて考えることができます。求めたいのは![]() となる確率、つまり図の青色部分の面積です。これは、次に示すように四角形の面積として求められます。
となる確率、つまり図の青色部分の面積です。これは、次に示すように四角形の面積として求められます。
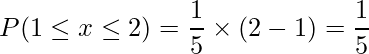
例題2:
0以上5以下の範囲で、乱数を10,000個作成したとき、その中で2以下の値をとる確率はいくらでしょうか。
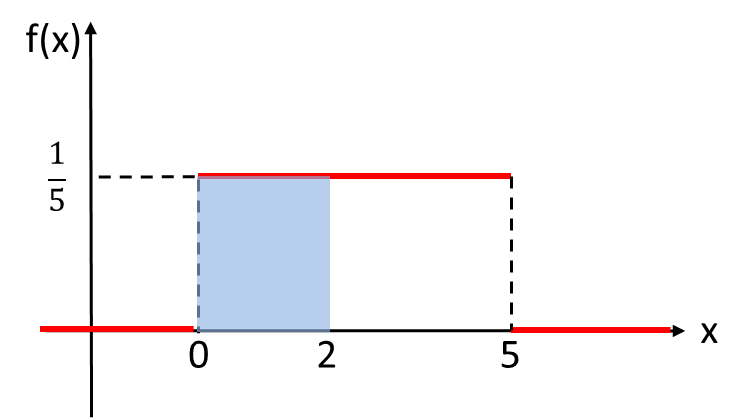
■四角形の面積として算出する場合
例題1と同じように四角形の面積として考えることができます。求めたいのは![]() となる確率、つまり図の青色の部分の面積です。したがって、次のように計算できます。
となる確率、つまり図の青色の部分の面積です。したがって、次のように計算できます。
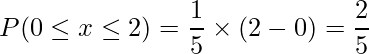
■累積分布関数を用いて算出する場合
この問題の場合、15-3章で学んだ累積分布関数を用いて算出することもできます。![]() のとき累積分布関数
のとき累積分布関数![]() は次の式で表せます。
は次の式で表せます。
この問題では、![]() 、
、![]() であることから、
であることから、
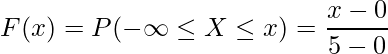
となります。求める確率は![]() となる確率であることから、
となる確率であることから、![]() を代入します。
を代入します。
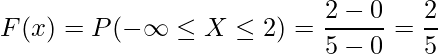
15. いろいろな確率分布3
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 12. 累積分布関数と確率変数の期待値・分散
12-1. 累積分布関数とは
- 15. いろいろな確率分布3
15-3. 連続一様分布1







