- Step1. 基礎編
- 15. いろいろな確率分布3
15-1. 指数分布
■指数分布
指数分布は連続型確率分布の一つで、機械が故障してから次に故障するまでの期間や、災害が起こってから次に起こるまでの期間のように、次に何かが起こるまでの期間が従う分布です。ある期間に平均して![]() (ラムダ)回起こる現象が、次に起こるまでの期間
(ラムダ)回起こる現象が、次に起こるまでの期間![]() が指数分布に従うとき、
が指数分布に従うとき、![]() となる確率密度関数
となる確率密度関数![]() は次の式で表されます。
は次の式で表されます。![]() は指数分布のパラメータであり、必ず正の値をとります。
は指数分布のパラメータであり、必ず正の値をとります。
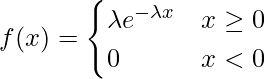
確率変数![]() が指数分布に従っている時、「
が指数分布に従っている時、「![]() 」と書きます。また、
」と書きます。また、![]() の期待値
の期待値![]() と分散
と分散![]() は次のようになります。
は次のようになります。
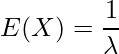
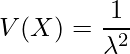
例えば、1時間に平均10人が来客するお店に、ある客が来てから次の客が来るまでの時間が5分となる確率密度を求めてみます。まず「時間」と「分」の単位を揃えるために5分を「1/12時間」とします。また、この例では![]() =10です。この
=10です。この![]() =1/12と
=1/12と![]() =10を確率密度関数
=10を確率密度関数![]() に代入すると、次のようになります。
に代入すると、次のようになります。
※この計算は、関数電卓もしくはExcelなどを使って行ってください。
■指数分布のグラフ
同様の計算を行い、次の客が来るまでの時間が0分から60分となる場合の確率密度を表にまとめました。
| 次に客が来るまでの時間 |
そのときの確率密度 | |
| 分 | 時間 | |
| 0 | 0.000 | 10.0 |
| 5 | 1/12 | 4.35 |
| 10 | 1/6 | 1.89 |
| 15 | 1/4 | 0.821 |
| 20 | 1/3 | 0.357 |
| 30 | 1/2 | 0.067 |
| 45 | 3/4 | 0.006 |
| 60 | 1 | 0.000 |
この表からグラフを描くと次のようになります。横軸は![]() を、縦軸は確率密度を表します。
を、縦軸は確率密度を表します。
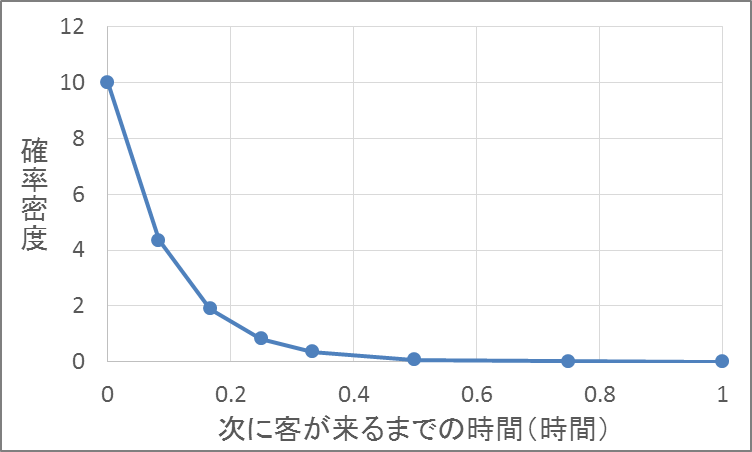
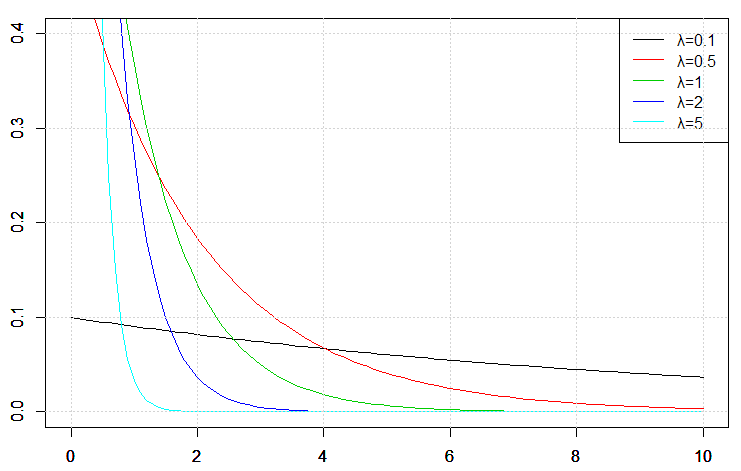
次に、さまざまな指数分布の形を見てみます。前述の例は![]() =10の指数分布を表したものでしたが、
=10の指数分布を表したものでしたが、![]() の値を0.1、0.5、1、2、5にした場合の指数分布は次のようになります。
の値を0.1、0.5、1、2、5にした場合の指数分布は次のようになります。
■指数分布の使い方
累積分布関数![]() は確率密度関数
は確率密度関数![]() を用いて算出できることは、12-1章で既に学びました。
を用いて算出できることは、12-1章で既に学びました。
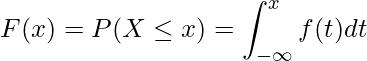
ただし、![]() は指数分布に従う確率変数
は指数分布に従う確率変数![]() の確率密度関数を表します。
の確率密度関数を表します。
ある期間に平均して![]() 回起こる現象が次に起こるまでの期間を
回起こる現象が次に起こるまでの期間を![]() としたとき、「期間
としたとき、「期間![]() が
が![]() 以下となる確率」、すなわち、「
以下となる確率」、すなわち、「![]() までの累積分布関数
までの累積分布関数![]() 」は次のようになります。
」は次のようになります。
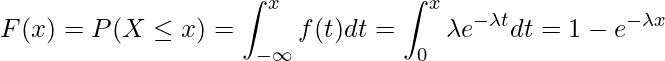
例題:
1時間に平均10人が来るお店に、ある客が来てから次の客が来るまでの時間が5分以内である確率はいくらでしょうか。
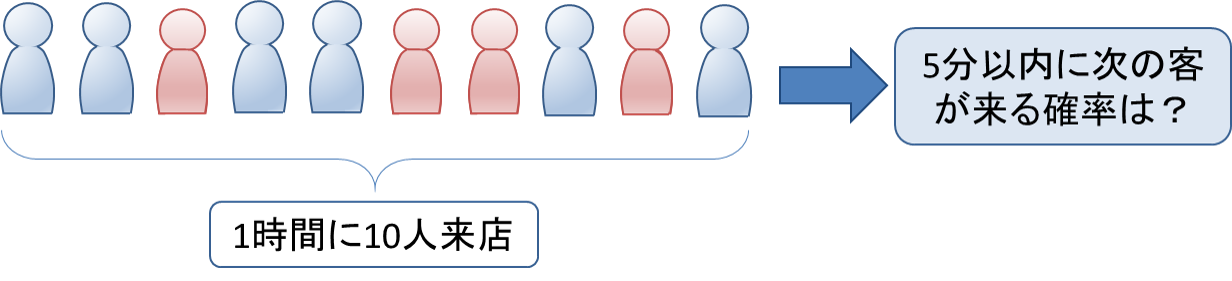
まずは単位を揃えます。5分=1/12時間なので、「次の客が来るまでの時間![]() =1/12時間以下となる確率」を求めます。問題文から
=1/12時間以下となる確率」を求めます。問題文から![]() =10です。
=10です。![]() に
に![]() と
と![]() の値を代入して計算すると約57%であることが分かります。
の値を代入して計算すると約57%であることが分かります。
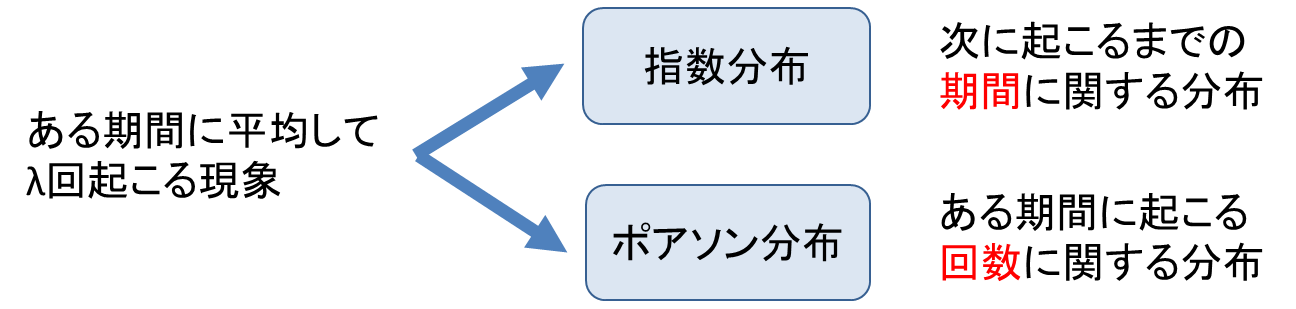
【コラム】指数分布とポアソン分布
指数分布は、13-3章で学んだポアソン分布と非常に似ていますが、ポアソン分布は「ある期間に平均して![]() 回起こる現象が、ある期間にちょうど
回起こる現象が、ある期間にちょうど![]() 回起きる確率の分布」のことです。
回起きる確率の分布」のことです。
■おすすめ書籍
演習に力を入れたい方はこちらをどうぞ。統計検定®2級対策本としてよく名前があがる本の1つです。
15. いろいろな確率分布3
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 9. 確率と期待値
9-6. 期待値
- 6. 分散と標準偏差
6-1. 分散
- 12. 累積分布関数と確率変数の期待値・分散
12-1. 累積分布関数とは
- 12. 累積分布関数と確率変数の期待値・分散
12-3. 確率変数の期待値
- 12. 累積分布関数と確率変数の期待値・分散
12-5. 確率変数の分散
- 13. いろいろな確率分布1
13-3. ポアソン分布








