- Step1. 基礎編
- 13. いろいろな確率分布1
13-3. ポアソン分布
■ポアソン分布の"素"となる二項分布
ある交差点で1年間のうち事故が起こる日数とその確率について考えます。これは、事故が起こるか起こらないかのベルヌーイ試行と考えることができます。ここでは1日に事故が起こる確率を![]() とします。このとき、1年間(
とします。このとき、1年間(![]() )のうち事故が起こる日数を確率変数
)のうち事故が起こる日数を確率変数![]() とすると、
とすると、![]() 日事故が起こる確率は二項分布の一般式にあてはめて次のように計算できます(ただし、1日に2回以上事故は起こらないものとします)。
日事故が起こる確率は二項分布の一般式にあてはめて次のように計算できます(ただし、1日に2回以上事故は起こらないものとします)。
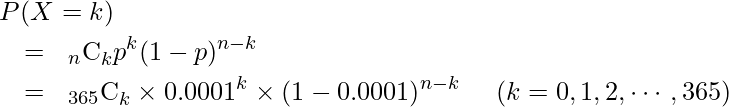
二項分布![]() では、確率変数
では、確率変数![]() の期待値は
の期待値は![]() によって求められることは13-2章で既に学びました。
によって求められることは13-2章で既に学びました。![]() はある事象が起こる平均回数を表します。
はある事象が起こる平均回数を表します。
■ポアソン分布
ここで![]() を一定の値「
を一定の値「![]() (ラムダ)」とおき、
(ラムダ)」とおき、![]() のままで
のままで![]() を十分大きく
を十分大きく![]() を十分に小さくした場合の二項分布は、平均
を十分に小さくした場合の二項分布は、平均![]() のポアソン分布に近似することができます。ポアソン分布は「ある期間に平均
のポアソン分布に近似することができます。ポアソン分布は「ある期間に平均![]() 回起こる現象が、ある期間に
回起こる現象が、ある期間に![]() 回起きる確率の分布」と言い換えられます。
回起きる確率の分布」と言い換えられます。

![]() がポアソン分布に従うとき、「
がポアソン分布に従うとき、「![]() 」と書きます。
」と書きます。![]() がポアソン分布でのパラメータです。確率変数
がポアソン分布でのパラメータです。確率変数![]() がポアソン分布に従う場合、ある期間に平均
がポアソン分布に従う場合、ある期間に平均![]() 回起こる現象が
回起こる現象が![]() 回起こる確率、すなわち
回起こる確率、すなわち![]() となる確率は次の式から計算できます。
となる確率は次の式から計算できます。
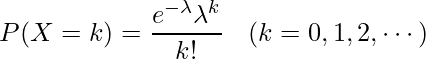
「![]() 」は「ネイピア数」あるいは「自然対数の底」と呼ばれる定数で、「
」は「ネイピア数」あるいは「自然対数の底」と呼ばれる定数で、「![]() 」という無限に続く値をもちます。
」という無限に続く値をもちます。
例題:
製品Aを作る工場では平均して200個に1個の割合で不良品が発生します。製造された製品Aを10個抜き取る時、この中に不良品が含まれる個数![]() がポアソン分布に従うとすると、不良品が1個含まれる(
がポアソン分布に従うとすると、不良品が1個含まれる(![]() となる)確率はいくらでしょうか。
となる)確率はいくらでしょうか。
不良品が発生する確率は![]() 、抜き取り検査をした個数は
、抜き取り検査をした個数は![]() であることから、
であることから、
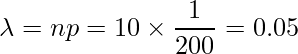
となります。したがって、
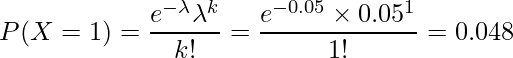
と計算され、10個の抜き取り検査で不良品が1個含まれる確率は約4.8%となります。
※この計算は、関数電卓もしくはExcelなどを使って行ってください。
■ポアソン分布のグラフ
同様の計算を行い、この製品Aの10個の抜き取り検査において![]() 個の不良品が含まれる確率を表にまとめました。
個の不良品が含まれる確率を表にまとめました。
| 不良品の個数 | 確率 |
|---|---|
| 0 | 0.951 |
| 1 | 0.048 |
| 2 | 0.001 |
| 3 | 0.000 |
| 4 | 0.000 |
| 5 | 0.000 |
| 6 | 0.000 |
| 7 | 0.000 |
| 8 | 0.000 |
| 9 | 0.000 |
| 10 | 0.000 |
この表からポアソン分布のグラフを描くと次のようになります。10個の抜き取り検査において不良品が1個も含まれない確率が最も高く、不良品の数が増えるほどその確率は低くなっていることが分かります。また、不良品が2個以上含まれる確率はほとんど0になっています。
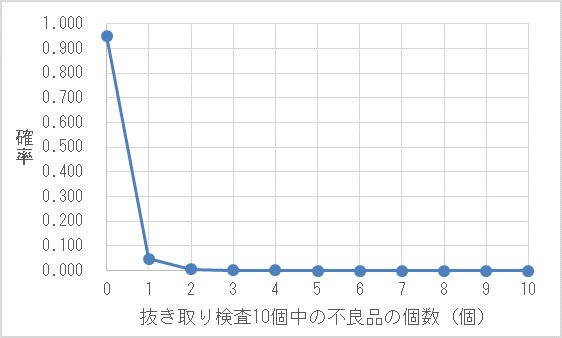
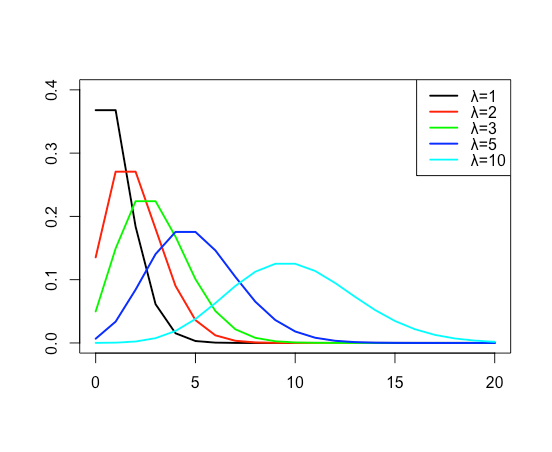
前述の例は![]() のときに抜き取り検査10個の中に含まれる不良品の個数の確率を表したものでした。次のグラフは、
のときに抜き取り検査10個の中に含まれる不良品の個数の確率を表したものでした。次のグラフは、![]() の値を1、2、3、5、10にした場合のポアソン分布のグラフです。横軸はある期間に平均して
の値を1、2、3、5、10にした場合のポアソン分布のグラフです。横軸はある期間に平均して![]() 回起こる現象が実際に起こる回数kを、縦軸はそのときの確率を表します。
回起こる現象が実際に起こる回数kを、縦軸はそのときの確率を表します。![]() が大きくなるほどグラフは右側へスライドし、右に裾を引いているグラフがだんだん左右対称に近づいていることが分かります。ポアソン分布は、
が大きくなるほどグラフは右側へスライドし、右に裾を引いているグラフがだんだん左右対称に近づいていることが分かります。ポアソン分布は、![]() が大きくなるにつれて正規分布に近づきます。
が大きくなるにつれて正規分布に近づきます。
【コラム】npとλのイメージ
ポアソン分布のパラメータ「![]() 」についてもう少し詳しく解説します。次の図の青の横線は「ある期間」、赤丸は「その期間内である事象が起こった時」を示しています。ここで「ある期間(青の横線)」を非常に細かく分割します。
」についてもう少し詳しく解説します。次の図の青の横線は「ある期間」、赤丸は「その期間内である事象が起こった時」を示しています。ここで「ある期間(青の横線)」を非常に細かく分割します。
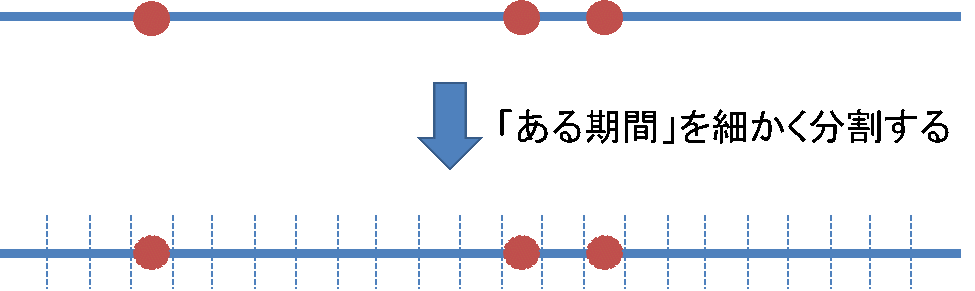
すると、分割した1つの期間内である事象が2回起こる確率は0と考えることができます。すなわち、分割した各期間の中で、ある事象が「起こった」か「起こらなかった」かのベルヌーイ試行と考えることができます。分割した期間が![]() 個である場合、ベルヌーイ試行を
個である場合、ベルヌーイ試行を![]() 回行う二項分布となります。
回行う二項分布となります。
分割した期間の中である事象が起こる確率を![]() とすると、二項分布の期待値である「ある期間に起こる事象の平均回数」は
とすると、二項分布の期待値である「ある期間に起こる事象の平均回数」は![]() と計算できます。この
と計算できます。この![]() を
を![]() (一定の値)とおき、
(一定の値)とおき、![]() 、
、![]() に近づけると、ある期間に平均
に近づけると、ある期間に平均![]() 回起こる事象がある期間に起こる回数
回起こる事象がある期間に起こる回数![]() が従う分布は「ポアソン分布」となります。
が従う分布は「ポアソン分布」となります。
■おすすめ書籍
このあたりの章までの復習にぜひ!
13. いろいろな確率分布1
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 13. いろいろな確率分布1
13-1. 二項分布
- 13. いろいろな確率分布1
13-2. 二項分布の期待値と分散
- ブログ
確率変数とは








