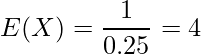- 13. いろいろな確率分布1
練習問題(13. いろいろな確率分布1)
1
さいころを10回振るとき、6の目が6回出る確率を求めよ。

答えを見る
- 答え:
 閉じる
閉じる -
さいころを1回振って、「6の目が出る事象」と「それ以外の目が出る事象」に分けることが出来るので、この確率は二項分布を用いて計算できます。6の目が出る確率は
 であるので、6の目が出る回数を
であるので、6の目が出る回数を とすると、
とすると、 は
は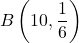 に従うと考えられます。よって、この確率は次のように計算できます。
に従うと考えられます。よって、この確率は次のように計算できます。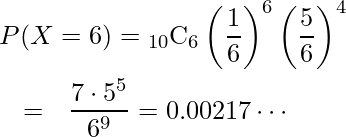
なお、この計算で実際に値を求めるのは暗算では難しいので、Excelの関数を使用すると簡単に計算できます。この場合、Binom.DIST関数を使用して、次のように入力すると確率を計算できます。
=BINOM.DIST(6,10,1/6,FALSE)
2
打率が3割のバッターが、5打席中3打席以上でヒットを打つ確率を求めよ。

答えを見る
- 答え:
 閉じる
閉じる -
「ヒットを打つ」か「打たない」かのいずれかの事象しかとらないため、この確率は二項分布を用いて計算できます。ヒットを打つ確率は3割=0.3であるので、ヒットを打つ回数を
 とすると、
とすると、 は
は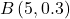 に従うと考えられます。
に従うと考えられます。- 5打席中3打席でヒットを打つ確率
- 5打席中4打席でヒットを打つ確率
- 5打席中5打席でヒットを打つ確率
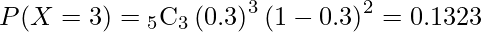
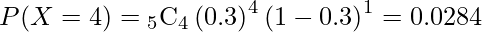
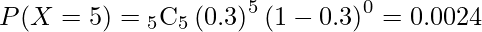
5打席中3打席以上ヒットを打つ確率は次のようになります。
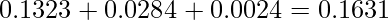
3
あるチョコレート菓子には当たりくじがついており、40個に1個の割合で当たりが入っていることが知られている。また、当たりくじを5つ集めると景品がもらえる。このチョコレート菓子を100個買ったときに、当たりくじが5つ含まれる確率はいくらか。ただし、当たりくじが含まれる数![]() はポアソン分布に従うものとする。
はポアソン分布に従うものとする。

答えを見る
- 答え:
 閉じる
閉じる -
ポアソン分布を用いて確率を計算します。
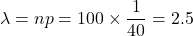 、
、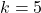 を使います。
を使います。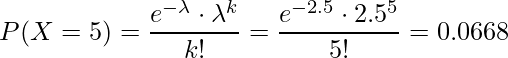
4
ある気まぐれな歌手について考える。彼は自身のコンサートでアンコールが起こっても、それに応えてもう一曲歌うのは稀で、およそ5%程度の確率でしか歌わないと言われている。彼が年間で40公演するとき、アンコールに応えて歌ってくれる公演数が3以上となる確率を求めよ。

答えを見る
- 答え
 閉じる
閉じる -
■二項分布を用いる場合
求める確率は、「アンコールに応えてくれる公演数が2以下となる事象」の余事象であることから、「0回応える確率」、「1回応える確率」、「2回応える確率」の和を1から引くことで計算できます。アンコールに応える回数を
 とすると
とすると は二項分布
は二項分布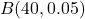 に従うことから、各々の確率は次のように計算できます。
に従うことから、各々の確率は次のように計算できます。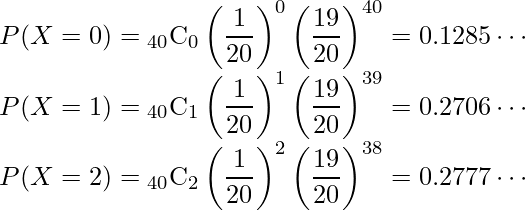
これらの和を1から引いたものが、求める確率となります。
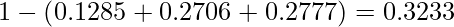
■ポアソン分布を用いる場合
この確率は、ポアソン分布を用いても計算できます。
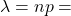 40公演×5%
40公演×5%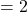 から、平均が2のポアソン分布で近似できると考えられます。
から、平均が2のポアソン分布で近似できると考えられます。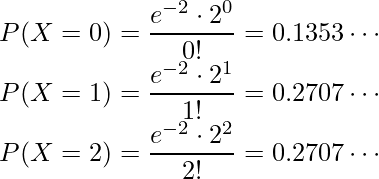
二項分布と同様に、これらの和を1から引くと求める確率となります。
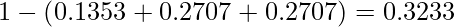
わずかに異なりますが、ほとんど同じ結果となることが分かります。
5
自転車に乗るのが大好きな太郎君が、1日のうちに自転車に乗って転んでしまう確率は25%であるという。転んだ日から次に転ぶ日までの平均日数はどのくらいであると期待されるか。ただし、転んだ日から次に転ぶ日までの日数![]() は幾何分布に従うものとする。
は幾何分布に従うものとする。

答えを見る
- 答え:
 閉じる
閉じる -
「自転車に乗って転ぶ」か「転ばない」かのベルヌーイ試行を繰り返す時、初めて転ぶまでの試行回数は幾何分布に従うと考えられます。
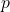 を転ぶ確率とすると、幾何分布の期待値
を転ぶ確率とすると、幾何分布の期待値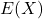 は次の式から求められます。
は次の式から求められます。
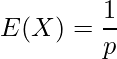
よって、次に転ぶまでの平均日数は次のように計算できます。