- Step1. 基礎編
- 14. いろいろな確率分布2
14-1. 正規分布
■正規分布
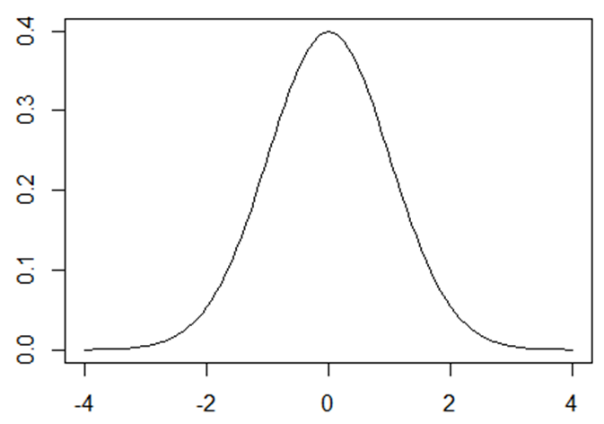
正規分布は統計学における検定や推定、モデルの作成など様々な場面で活用される連続型確率分布です。多くの統計的手法において、データが正規分布に従うことを仮定します。正規分布は次の図のように左右対称の形をしており、横軸は確率変数を、縦軸はそのときの確率密度を表します。
正規分布に従う確率変数![]() の確率密度関数
の確率密度関数![]() は次の式で表されます。
は次の式で表されます。
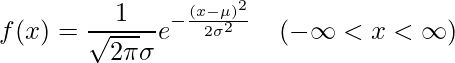
この式の「![]() 」に「
」に「![]() 」を使うと次のように表すこともできます。
」を使うと次のように表すこともできます。
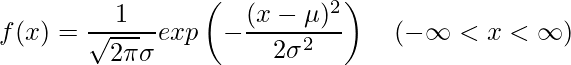
「![]() (シグマ)」と「
(シグマ)」と「![]() (ミュー)」が正規分布のパラメータ(母数)です。確率変数
(ミュー)」が正規分布のパラメータ(母数)です。確率変数![]() の期待値と分散は次のようになります。
の期待値と分散は次のようになります。
したがって、確率変数![]() は「平均
は「平均![]() 、分散
、分散![]() の正規分布に従う」と言えます。このとき、「
の正規分布に従う」と言えます。このとき、「![]() 」と書きます。
」と書きます。
■正規分布のグラフ
例えば、あるクラスの生徒のテストの点数![]() が平均
が平均![]() 点、標準偏差
点、標準偏差![]() 点(分散
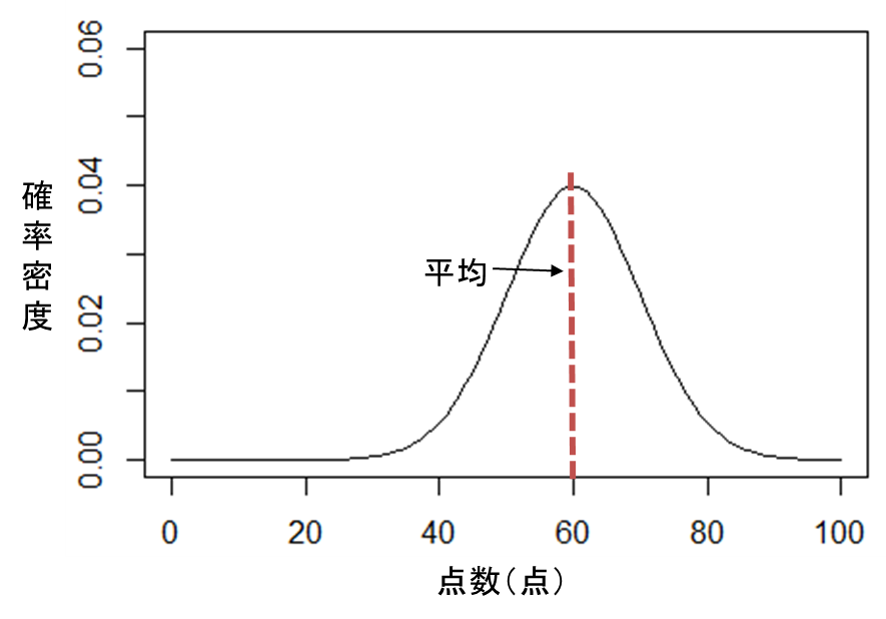
点(分散![]() )の正規分布に従う時、その確率密度関数は次の図のようになります。確率密度は、平均点である
)の正規分布に従う時、その確率密度関数は次の図のようになります。確率密度は、平均点である![]() 点(横軸が
点(横軸が![]() )の部分が最も高く、平均から左右に離れるにつれて低くなっていることが分かります。
)の部分が最も高く、平均から左右に離れるにつれて低くなっていることが分かります。
次に、さまざまな正規分布の形を見てみます。前述の例は平均が![]() 点、標準偏差が
点、標準偏差が![]() 点の正規分布を表したものでしたが、平均値
点の正規分布を表したものでしたが、平均値![]() を
を![]() に固定し、標準偏差
に固定し、標準偏差![]() の値を
の値を![]() 、
、![]() 、
、![]() 、
、![]() 、
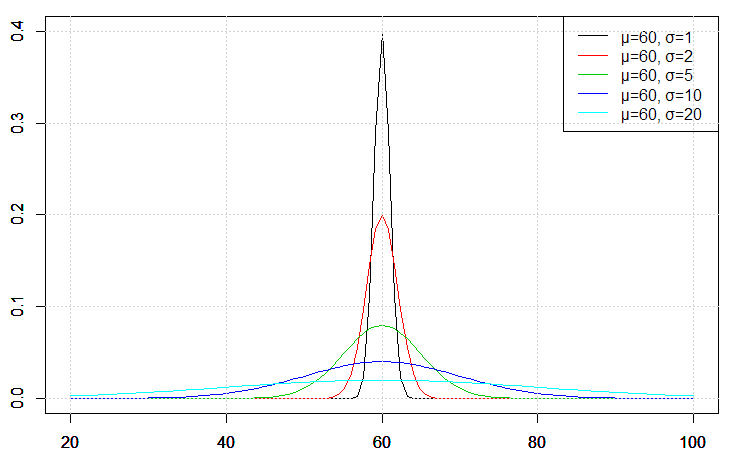
、![]() にした場合の正規分布は次の図のようになります。
にした場合の正規分布は次の図のようになります。![]() が大きいほど分布の山がなだらかになることが分かります。
が大きいほど分布の山がなだらかになることが分かります。
また、標準偏差を固定し平均値![]() を変化させたとき、その大小で正規分布の分布の山がどのように変化するかを表したものが次の図です。このグラフでは標準偏差を
を変化させたとき、その大小で正規分布の分布の山がどのように変化するかを表したものが次の図です。このグラフでは標準偏差を![]() に固定し、平均値
に固定し、平均値![]() の値を
の値を![]() 、
、![]() 、
、![]() 、
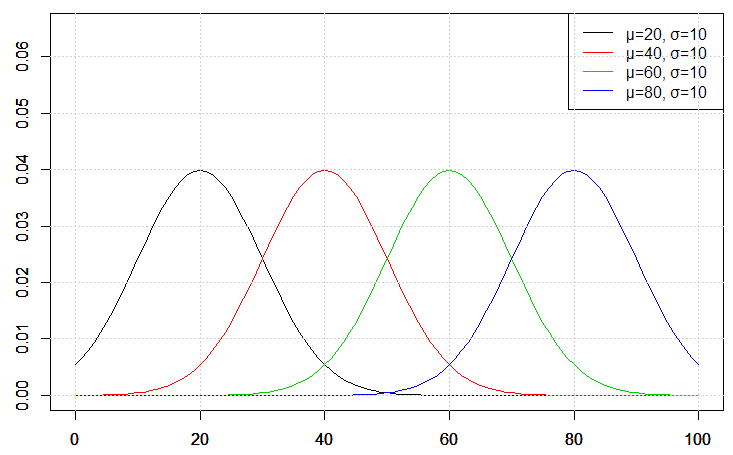
、![]() にしています。正規分布の山頂のx軸座標は
にしています。正規分布の山頂のx軸座標は![]() の値と等しくなるので、
の値と等しくなるので、![]() が大きくなるほどグラフは右側へスライドします。
が大きくなるほどグラフは右側へスライドします。
※ここではテストの点数を連続型確率分布である「正規分布」に従うと仮定しています。テストの点数は整数の値しか取らないので厳密には「離散型変数」ですが、取りうる値が多い(0点から100点まで1点刻みの値がある)ことから、便宜的に「連続型変数」と考えて統計解析を行うことができます。
【コラム】Bell curveの由来
正規分布は平均を中心に左右対称で、教会にある「ベル(釣鐘)」のような形をしていることから、「ベルカーブ(bell curve)」ともよばれます。
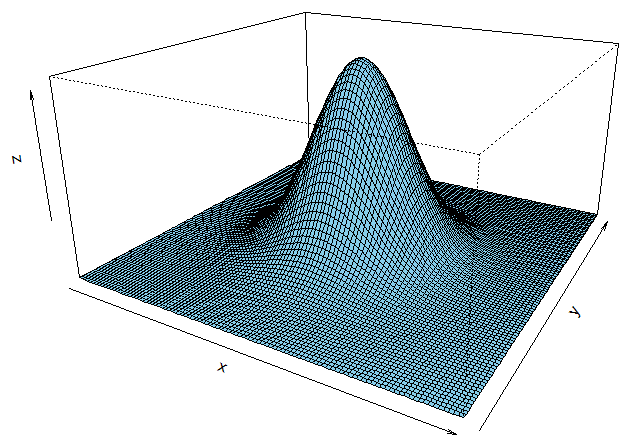
正規分布の曲線を描く式は、1733年にフランスのド・モアブルが考案しました。1812年にラプラスが式を完成させたので、この式はド・モアブル-ラプラスの定理として知られています。この式によって得られる確率分布に正規分布の名前が付いたのは1875年のことです。正規分布を釣鐘のようだと思う人はそれ以前からいました。Esprit Jouffret は1872年に書いた論文の中で、次の2変数正規分布の姿を"bell surface"と表現しています。確かに釣鐘のように見えます。
■おすすめ書籍
ちょうどこの章(正規分布)までの内容を網羅しています。数学が苦手な方は一度手にとってみることをおすすめします。
14. いろいろな確率分布2
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 6. 分散と標準偏差
6-2. 標準偏差
- 11. 確率変数と確率分布
11-4. 確率密度と確率密度関数
- 12. 累積分布関数と確率変数の期待値・分散
12-3. 確率変数の期待値
- 12. 累積分布関数と確率変数の期待値・分散
12-5. 確率変数の分散
- ブログ
正規分布の発見








