- Step1. 基礎編
- 14. いろいろな確率分布2
14-2. 正規分布の再生性と標準正規分布
■正規分布の再生性
正規分布![]() に従うあるデータと、そのデータとは独立な正規分布
に従うあるデータと、そのデータとは独立な正規分布![]() に従うデータを足したデータは、正規分布
に従うデータを足したデータは、正規分布![]() に従います。これを正規分布の再生性といいます。
に従います。これを正規分布の再生性といいます。
例えば、あるクラスの数学と国語のテストの結果は次の通りでした。
- 数学 平均点
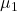 :
: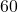 点 標準偏差
点 標準偏差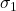 :
: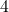 点
点 - 国語 平均点
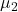 :
: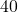 点 標準偏差
点 標準偏差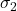 :
: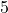 点
点
このクラスの数学および国語の点数はそれぞれ異なる(独立な)正規分布に従うとき、数学と国語の点数を足した点数は、平均が![]() 、分散が
、分散が![]() の正規分布
の正規分布![]() に従います。
に従います。
■標準正規分布
正規分布の中で、特に「平均![]() 、分散
、分散![]() 」である正規分布を「標準正規分布」といいます。確率変数
」である正規分布を「標準正規分布」といいます。確率変数![]() が標準正規分布に従う時、
が標準正規分布に従う時、![]() と書きます。
と書きます。

正規分布に従う確率変数![]() の確率密度関数
の確率密度関数![]() の式は14-1章で既に学びました。この式に「
の式は14-1章で既に学びました。この式に「![]() 、
、![]() 」を代入すると、次のようになります。
」を代入すると、次のようになります。
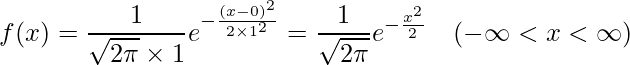
したがって、標準正規分布に従う確率変数![]() の確率密度関数
の確率密度関数![]() は次式で表せます。
は次式で表せます。
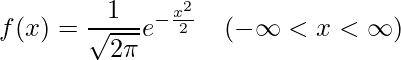
あるいは「![]() 」を使うと次のように表すこともできます。
」を使うと次のように表すこともできます。
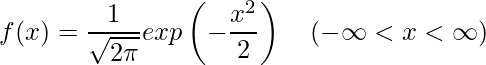
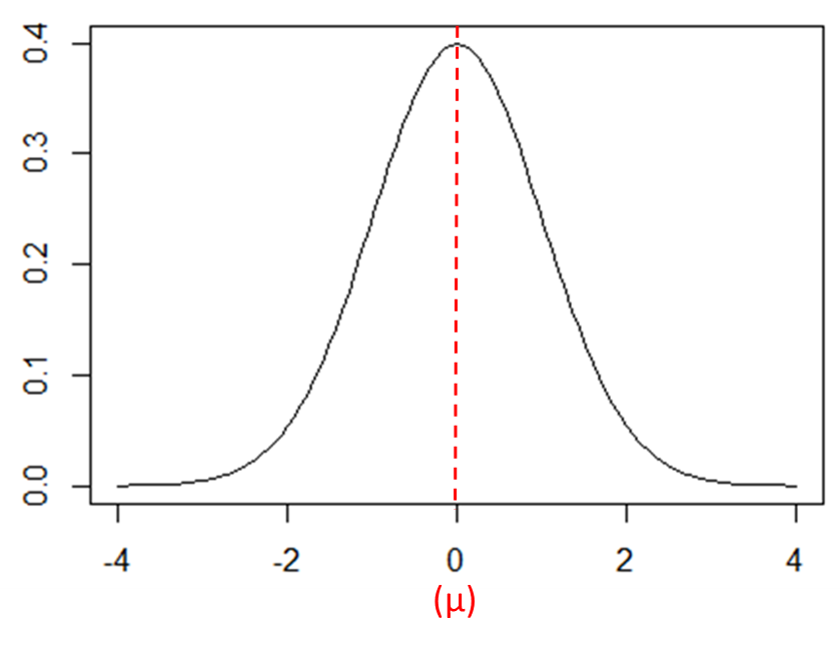
次のグラフは標準正規分布を表したものです。平均![]() であることから、分布の山頂にあたる
であることから、分布の山頂にあたる![]() 軸座標の値は「
軸座標の値は「![]() 」です。
」です。
14. いろいろな確率分布2
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 6. 分散と標準偏差
6-1. 分散
- 6. 分散と標準偏差
6-2. 標準偏差
- 14. いろいろな確率分布2
14-1. 正規分布
- ブログ
正規分布の発見







