ある確率変数が平均、分散の正規分布に従う時、から平均を引いて標準偏差（※ 標準偏差＝√分散）で割った値をとおくと、は「平均が、分散がの標準正規分布」に従います。したがって、標準化を行うことにより、単位や平均値などが異なるデータ同士を単純に比較できるようになります。

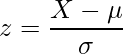
このような計算（データ変換）のことを「標準化」といいます。標準化した値を「値」、あるいは「標準化得点」と呼びます。

例題：

あるクラスの数学と国語のテストの結果は次の通りでした。

• 数学　平均点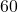：点　標準偏差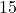：点
• 国語　平均点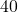：点　標準偏差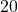：点

太郎君は数学が点、国語が点でした。順位がより上なのはどちらの教科でしょうか。ただし、このクラスの数学および国語の点数はそれぞれ異なる（独立な）正規分布に従うものとします。

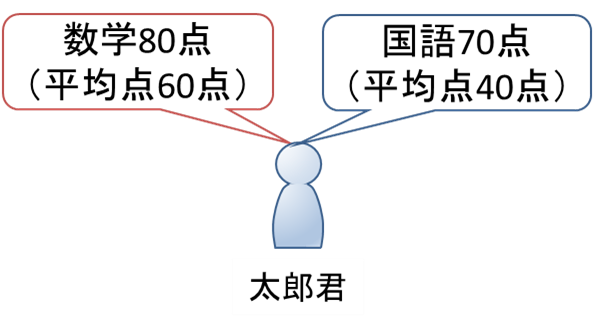
点数だけを見ると、数学のほうが国語に比べて高くなっています。一方、国語のほうが数学に比べて平均点が低いので、国語のほうが平均点に対して良い点数をとっているとも言えそうです。このような場合には、それぞれの点数を標準化して比較します。

• 数学の点数（数学：、）

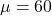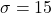• 国語の点数（国語：、）

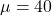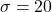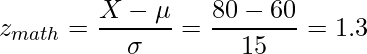
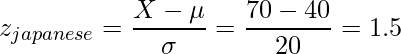
したがって、となりました。標準化した値が大きいほど相対的な順位が高いことを示すので、太郎君の場合は数学よりも国語の方が順位は高いと言えます。

試験や模試の結果で登場する「偏差値」も、この標準化した値を用いて次の式から求められます。偏差値は「平均が点、標準偏差が点」となるように、標準化した値にをかけてを足したものです。

太郎君のテスト結果から偏差値を算出してみます。

• 数学の偏差値：
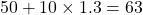
• 国語の偏差値：

【コラム】偏差値は100を超える！？

偏差値は、試験や模試を受けた後に気になるものの1つではないでしょうか。偏差値は、教科ごとの点数の分布を「平均が点、標準偏差が点」になるように変換した値です。もし平均点と同じ点数をとった場合、標準化した値は次のようにになるため、偏差値はになります。

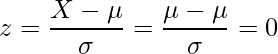
次に平均点20点、標準偏差15点という試験で100点をとった場合の偏差値を計算してみます。このときの偏差値は以下のように103となり、100を超えます。

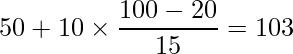
このように、偏差値はテストの点数と異なりを超えることがあります。これは計算間違いなどではなく、多くの受験生がほとんど同じような点数をとり（標準偏差が小さい）、かつ平均点が低い場合に高得点を取ると起こり得ます。また、偏差値が未満となる場合もあります。