- Step1. 基礎編
- 14. いろいろな確率分布2
14-6. 標準正規分布の使い方2
例題:
あるクラスの試験結果は平均72.8点、標準偏差15点の正規分布に従っています。この時、70点から90点の人は何%いるでしょうか。

この問題も標準正規分布を使って計算できます。ただし、次の流れで計算をする必要があります。
(i) 70点以上の人の割合を算出
(ii) 90点以上の人の割合を算出
(iii) (i)の割合から(ii)の割合を引いて、70点から90点の人の割合を算出
(i) 70点以上の人の割合を算出
「70点」を標準化します。
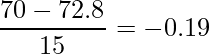
標準正規分布表には負の値はありませんが、標準正規分布は![]() に対して左右対称なので、負の値「-0.19」は正の値「0.19」として考えます。統計数値表から「0.19」の値は「0.425」と読み取れます。
に対して左右対称なので、負の値「-0.19」は正の値「0.19」として考えます。統計数値表から「0.19」の値は「0.425」と読み取れます。
| z | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 0.496 | 0.492 | 0.488 | 0.484 | 0.48 | 0.476 | 0.472 | 0.468 | 0.464 |
| 0.1 | 0.46 | 0.456 | 0.452 | 0.448 | 0.444 | 0.44 | 0.436 | 0.433 | 0.429 | 0.425 |
| 0.2 | 0.421 | 0.417 | 0.413 | 0.409 | 0.405 | 0.401 | 0.397 | 0.394 | 0.39 | 0.386 |
| 0.3 | 0.382 | 0.378 | 0.374 | 0.371 | 0.367 | 0.363 | 0.359 | 0.356 | 0.352 | 0.348 |
| 0.4 | 0.345 | 0.341 | 0.337 | 0.334 | 0.33 | 0.326 | 0.323 | 0.319 | 0.316 | 0.312 |
| 0.5 | 0.309 | 0.305 | 0.302 | 0.298 | 0.295 | 0.291 | 0.288 | 0.284 | 0.281 | 0.278 |
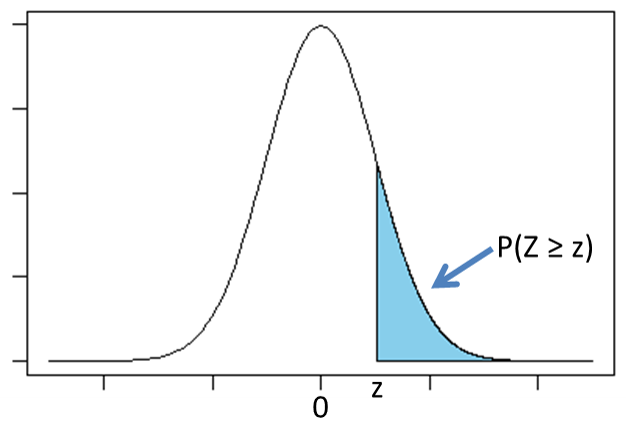
「0.425」は、次の図に示すように「標準正規分布に従うZがとる値が0.19以上となる確率![]() 」です。この確率は「Zがとる値が-0.19以下となる確率
」です。この確率は「Zがとる値が-0.19以下となる確率![]() 」と等しくなります。今求めたいのは70点以上となる確率、すなわちZがとる値が-0.19以上となる確率
」と等しくなります。今求めたいのは70点以上となる確率、すなわちZがとる値が-0.19以上となる確率![]() なので、次のグラフの白色部分の面積を求めます。
なので、次のグラフの白色部分の面積を求めます。
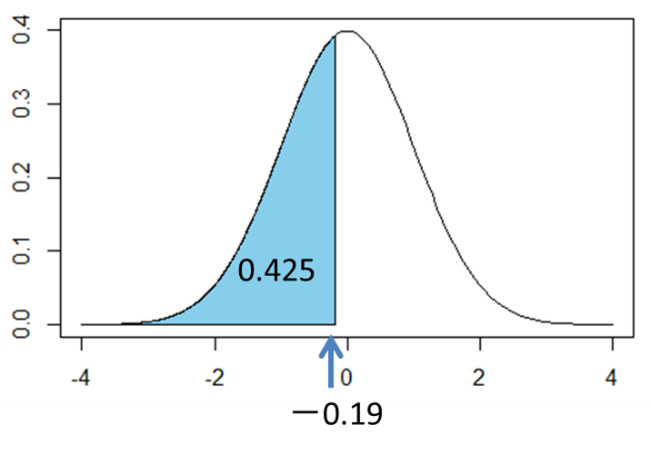
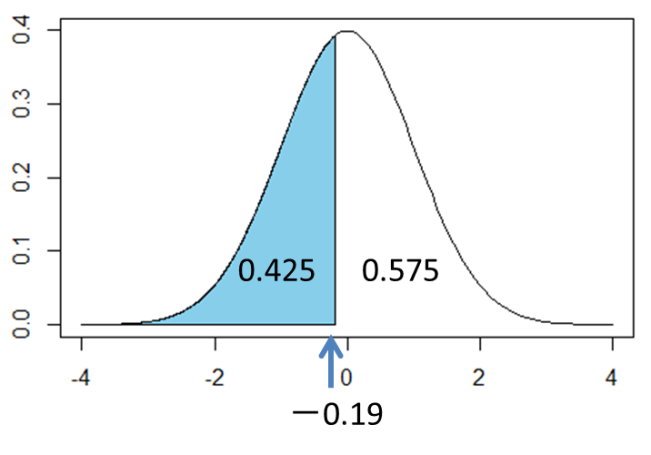
![]() 軸と標準正規分布で囲まれた部分の面積は1です。したがって
軸と標準正規分布で囲まれた部分の面積は1です。したがって![]() より、70点以上の人の割合は0.575と算出されます。
より、70点以上の人の割合は0.575と算出されます。
(ii) 90点以上の人の割合を算出
「90点」を標準化します。
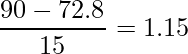
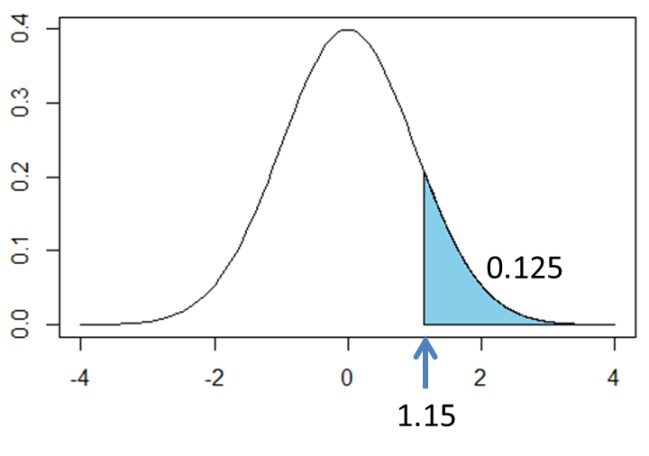
標準正規分布表の「1.15」の値を読み取ると「0.125」です。これはZがとる値が1.15より大きくなる確率![]() 、すなわち90点以上の人の割合です。
、すなわち90点以上の人の割合です。
| z | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 0.496 | 0.492 | 0.488 | 0.484 | 0.48 | 0.476 | 0.472 | 0.468 | 0.464 |
| 0.1 | 0.46 | 0.456 | 0.452 | 0.448 | 0.444 | 0.44 | 0.436 | 0.433 | 0.429 | 0.425 |
| 0.2 | 0.421 | 0.417 | 0.413 | 0.409 | 0.405 | 0.401 | 0.397 | 0.394 | 0.39 | 0.386 |
| 0.3 | 0.382 | 0.378 | 0.374 | 0.371 | 0.367 | 0.363 | 0.359 | 0.356 | 0.352 | 0.348 |
| 0.4 | 0.345 | 0.341 | 0.337 | 0.334 | 0.33 | 0.326 | 0.323 | 0.319 | 0.316 | 0.312 |
| 0.5 | 0.309 | 0.305 | 0.302 | 0.298 | 0.295 | 0.291 | 0.288 | 0.284 | 0.281 | 0.278 |
| 0.6 | 0.274 | 0.271 | 0.268 | 0.264 | 0.261 | 0.258 | 0.255 | 0.251 | 0.248 | 0.245 |
| 0.7 | 0.242 | 0.239 | 0.236 | 0.233 | 0.23 | 0.227 | 0.224 | 0.221 | 0.218 | 0.215 |
| 0.8 | 0.212 | 0.209 | 0.206 | 0.203 | 0.2 | 0.198 | 0.195 | 0.192 | 0.189 | 0.187 |
| 0.9 | 0.184 | 0.181 | 0.179 | 0.176 | 0.174 | 0.171 | 0.169 | 0.166 | 0.164 | 0.161 |
| 1 | 0.159 | 0.156 | 0.154 | 0.152 | 0.149 | 0.147 | 0.145 | 0.142 | 0.14 | 0.138 |
| 1.1 | 0.136 | 0.133 | 0.131 | 0.129 | 0.127 | 0.125 | 0.123 | 0.121 | 0.119 | 0.117 |
| 1.2 | 0.115 | 0.113 | 0.111 | 0.109 | 0.107 | 0.106 | 0.104 | 0.102 | 0.1 | 0.099 |
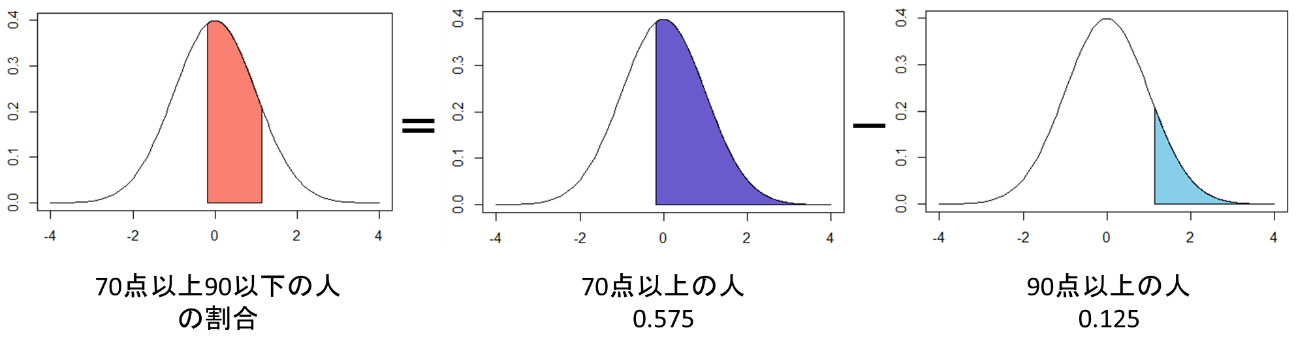
(iii) (i)の割合から(ii)の割合を引いて、70点から90点の人の割合を算出
最後に、次の図の橙色部分の確率![]() を求めます。この確率は
を求めます。この確率は![]() と算出されます。したがって、答えは45.0%となります。
と算出されます。したがって、答えは45.0%となります。
14. いろいろな確率分布2
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 14. いろいろな確率分布2
14-5. 標準正規分布表の使い方1
- ブログ
正規分布の発見







