- Step1. 基礎編
- 14. いろいろな確率分布2
14-4. 標準正規分布表
累積分布関数![]() は確率密度関数
は確率密度関数![]() を用いて算出できることは12-1章で既に学びました。
を用いて算出できることは12-1章で既に学びました。
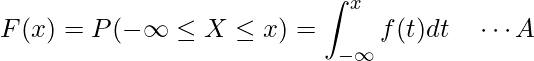
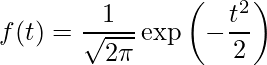
例えばA式の![]() に-2を代入すると、確率変数
に-2を代入すると、確率変数![]() のとる値が-2以下となる確率を算出できます。
のとる値が-2以下となる確率を算出できます。
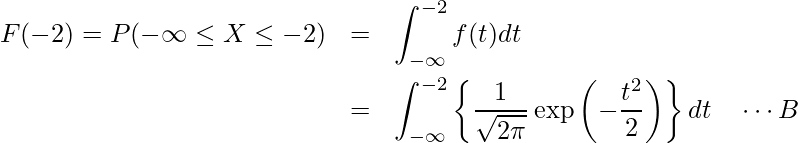
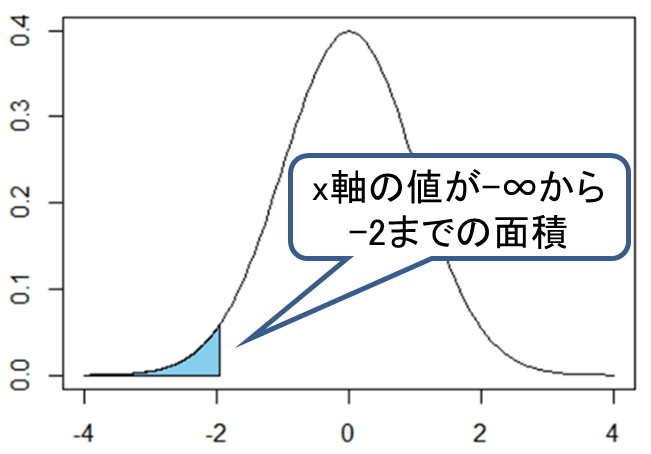
B式を計算すると![]() となります。これは次に示す標準正規分布の水色部分の面積、すなわち標準正規分布において
となります。これは次に示す標準正規分布の水色部分の面積、すなわち標準正規分布において![]() 軸の値が-2以下となる確率が「0.023」であるということを意味します。
軸の値が-2以下となる確率が「0.023」であるということを意味します。
B式を見ると分かるように、累積分布関数を計算するのは非常に面倒であるため、次の表のような「標準正規分布表」とよばれる統計数値表が用意されています。標準正規分布表には、標準正規分布における![]() 軸の様々な値以上もしくは以下(
軸の様々な値以上もしくは以下(![]() で表します)となる確率がまとめられています。
で表します)となる確率がまとめられています。
| z | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | … |
|---|---|---|---|---|---|---|---|
| 0 | 0.5 | 0.496 | 0.492 | 0.488 | 0.484 | 0.48 | … |
| 0.1 | 0.46 | 0.456 | 0.452 | 0.448 | 0.444 | 0.44 | … |
| 0.2 | 0.421 | 0.417 | 0.413 | 0.409 | 0.405 | 0.401 | … |
| 0.3 | 0.382 | 0.378 | 0.374 | 0.371 | 0.367 | 0.363 | … |
| 0.4 | 0.345 | 0.341 | 0.337 | 0.334 | 0.33 | 0.326 | … |
| 0.5 | 0.309 | 0.305 | 0.302 | 0.298 | 0.295 | 0.291 | … |
| ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ | ︙ |
統計数値表には、標準正規分布表の他に![]() 分布表・
分布表・![]() 分布表・カイ二乗分布表などいくつかの種類があります。これらの統計数値表も標準正規分布表と同様に、各々の分布における
分布表・カイ二乗分布表などいくつかの種類があります。これらの統計数値表も標準正規分布表と同様に、各々の分布における![]() 軸の様々な値以上もしくは以下となる確率が示されています。データの分布に合わせた統計数値表を使用することで、複雑な計算をすること無く、ある分布における求めたい確率を得ることができます。
軸の様々な値以上もしくは以下となる確率が示されています。データの分布に合わせた統計数値表を使用することで、複雑な計算をすること無く、ある分布における求めたい確率を得ることができます。
■おすすめ書籍
個人的にとてもおすすめのシリーズです。間違いなく読みやすいです。
14. いろいろな確率分布2
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 14. いろいろな確率分布2
14-2. 正規分布の再生性と標準正規分布
- ブログ
正規分布の発見








