- 14. いろいろな確率分布2
練習問題(14. いろいろな確率分布2)
1
日本人男性2人をランダムに選んで肩車をしてもらった時、身長はどのような分布となるか求めよ。ただし、日本人男性の肩までの身長は正規分布![]() 、座高は正規分布
、座高は正規分布![]() に従うとし、肩車をした時の身長は(肩までの身長)+(座高)で計算できるものとする。
に従うとし、肩車をした時の身長は(肩までの身長)+(座高)で計算できるものとする。

答えを見る
- 答え
 閉じる
閉じる -
下側の男性の肩までの身長を
 、上側の男性の座高を
、上側の男性の座高を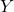 とすると、肩車をした身長は
とすると、肩車をした身長は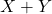 の分布に従います。これは和の分布であり、XとYはどちらも正規分布に従うことから、
の分布に従います。これは和の分布であり、XとYはどちらも正規分布に従うことから、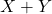 もまた正規分布に従います。正規分布の再生性により、X+Yの分布は次のように計算できます。
もまた正規分布に従います。正規分布の再生性により、X+Yの分布は次のように計算できます。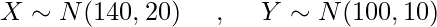
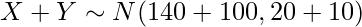
したがって、肩車した時の身長は平均240、分散30の正規分布
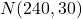 に従います。
に従います。
2
確率変数![]() が標準正規分布
が標準正規分布![]() に従うとき、
に従うとき、![]() が2以上となる確率
が2以上となる確率![]() を標準正規分布表から求めよ。
を標準正規分布表から求めよ。

答えを見る
- 答え
 閉じる
閉じる -
標準正規分布表の使い方についての問題です。14-5章で示した標準正規分布表(上側確率についての標準正規分布表)には
 がとる値が
がとる値が 以上となる確率
以上となる確率 が示されています。この表から
が示されています。この表から =2.00となる数値を探すと、「0.023」という値が得られます。したがって、答えは2.3%となります。
=2.00となる数値を探すと、「0.023」という値が得られます。したがって、答えは2.3%となります。
3
確率変数![]() が標準正規分布
が標準正規分布![]() に従うとき、
に従うとき、![]() が
が![]() 以上となる確率
以上となる確率![]() が10%となるような
が10%となるような![]() を標準正規分布表から求めよ。
を標準正規分布表から求めよ。

答えを見る
- 答え
 閉じる
閉じる -
標準正規分布表のもう一つの使い方についての問題です。14-1章で示した標準正規分布表(上側確率についての標準正規分布表)から0.10に最も近い値を探し、その値に対応するzの値を読み取ったものが答えです。
表を探すと、0.1003が最も0.10に近い値であると読み取れます。次に、その値の行と列の表頭と表側を読み取ります。
 =1.2の行の、0.08の列であることから、
=1.2の行の、0.08の列であることから、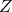 がとる値が
がとる値が =1.28以上となる確率が約0.10であることが分かります。
=1.28以上となる確率が約0.10であることが分かります。
4
日本人男性の平均身長が正規分布![]() に従うと仮定し、次の3つの割合を求めよ。
に従うと仮定し、次の3つの割合を求めよ。
- 平均身長以下の人の割合
- 平均±1標準偏差の間に収まる人の割合
- 180cm以上となる人の割合

答えを見る
- 答え
 閉じる
閉じる -
標準化した値を使って、標準正規分布表からそれぞれの数値を読み取ります。基準化した値
 は次の式から計算できます。
は次の式から計算できます。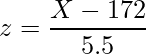
1:
 =172として標準化すると、
=172として標準化すると、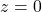 となります。このとき、標準正規分布に従う
となります。このとき、標準正規分布に従う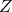 が0以上の値をとる確率
が0以上の値をとる確率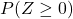 は標準正規分布表より0.5です。
は標準正規分布表より0.5です。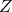 が0以下の値をとる確率
が0以下の値をとる確率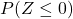 は余事象から
は余事象から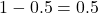 と求められます。したがって、身長が正規分布に従うとき、平均身長以下の人は50%となります。
と求められます。したがって、身長が正規分布に従うとき、平均身長以下の人は50%となります。
2:平均±1標準偏差となる身長は、それぞれ
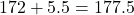 、
、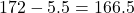 となります。この値を標準化すると、
となります。この値を標準化すると、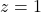 と
と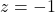 であることから、求める確率は
であることから、求める確率は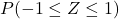 となります。標準正規分布は
となります。標準正規分布は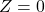 に対して左右対称であることから、次のように変形することができます。
に対して左右対称であることから、次のように変形することができます。
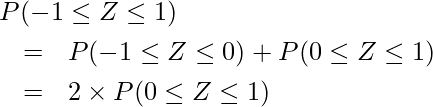
また、累積分布関数の性質から、
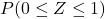 は次のように変形することができます。
は次のように変形することができます。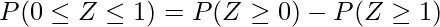
標準正規分布表から、
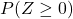 と
と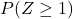 となる確率を読み取ると、それぞれ「0.5」、「0.1587」です。以上から、
となる確率を読み取ると、それぞれ「0.5」、「0.1587」です。以上から、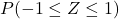 は次のように求められます。
は次のように求められます。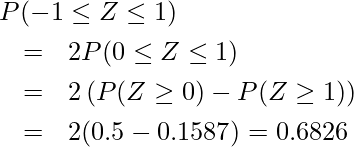
日本人男性の身長が正規分布に従う場合、平均身長から1標準偏差の範囲におよそ70%の人がいることが分かりました。これは正規分布に関わる重要な性質で、覚えておくと便利です。
3:
 =180として標準化すると、
=180として標準化すると、 =1.45となります。対応する値を標準正規分布表から読み取ると、「0.0735」です。したがって、180cm以上の高身長の男性は、全体の7.4%しかいないことが分かります。
=1.45となります。対応する値を標準正規分布表から読み取ると、「0.0735」です。したがって、180cm以上の高身長の男性は、全体の7.4%しかいないことが分かります。
5
ある模擬試験でA君の成績は英語79点、数学82点であった。
- 英語の平均点は85点、標準偏差は4点の正規分布に従うものとする。A君の成績は下からどれくらいの順位か。
- 数学では、A君の成績は上位約5%の順位であった。数学の標準偏差が10点であるとき、数学の平均点はどれくらいか。なお、数学の点数の分布は正規分布に従うものとする。

答えを見る
- 答え
 閉じる
閉じる -
1:英語の点数を標準化して、標準正規分布の上で考えます。標準化すると、
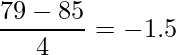
となります。標準正規分布は0を中心に左右対称なので、「-1.5」は「1.5」として考えることができます。「1.5」のところを見ると0.0668なのでA君の成績は下位0.0668、すなわち6.7%くらいであることが分かります。
2:標準正規分布表(上側確率)で「0.05(5%)」となるところは1.64なので、数学の平均点を
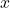 点とおくと、標準化の式は
点とおくと、標準化の式は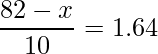
です。
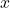 を求めると、
を求めると、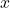 ≒66点となります。
≒66点となります。







