- Step1. 基礎編
- 14. いろいろな確率分布2
14-5. 標準正規分布表の使い方1
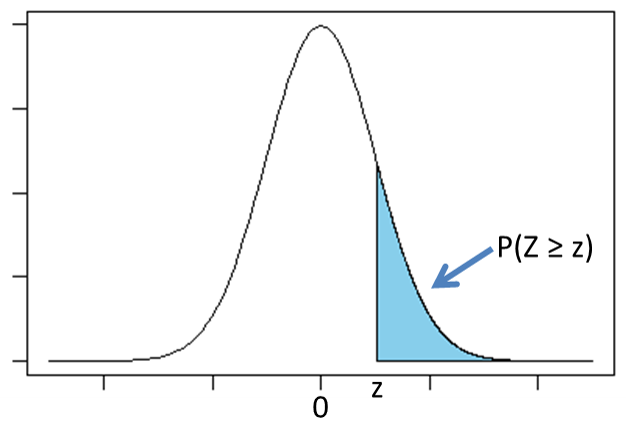
あるデータが正規分布に従うと仮定できる場合、このデータを標準化することで「標準正規分布表」を用いて確率を求めることができます。例えば標準正規分布表に次のような図が描かれている場合、表の値は水色部分の面積を表します。これは、「標準正規分布に従うZがとる値がz以上となる確率![]() 」を意味します。
」を意味します。
例題:
あるクラスのテスト結果は平均72.8点、標準偏差15点の正規分布に従っています。この時、88点以上の人は何%いるでしょうか。
まず88点を標準化すると、次のようになります。
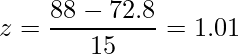
次に、Zがとる値が1.01以上となる確率を求めます。この確率を求めるため、「1.01」を標準正規分布表に当てはめます。当てはめる値は「小数点第1位以上」と「小数点第2位以下」に分ける必要があるため、「1.01」を「1.0」と「0.01」に分けます。
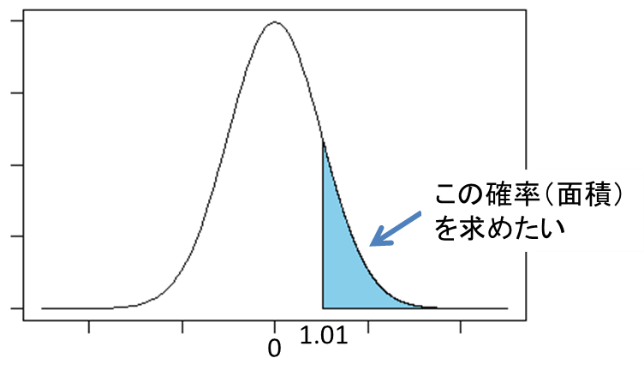
小数点第1位以上の「1.0」は、標準正規分布表の左端の列の「1.0」の行を見ます(赤色行)。小数点第2位以下の「0.01」は、上端の行の中から「.01(=0.01)」の列を見ます(青色列)。行と列が重なる部分(紫色セル)の値である「0.156」が、Zがとる値が1.01以上となる場合の確率![]() です。したがって、88点以上の人は15.6%いるということが分かります。
です。したがって、88点以上の人は15.6%いるということが分かります。
| z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.500 | 0.496 | 0.492 | 0.488 | 0.484 | 0.480 | 0.476 | 0.472 | 0.468 | 0.464 |
| .1 | 0.460 | 0.456 | 0.452 | 0.448 | 0.444 | 0.440 | 0.436 | 0.433 | 0.429 | 0.425 |
| .2 | 0.421 | 0.417 | 0.413 | 0.409 | 0.405 | 0.401 | 0.397 | 0.394 | 0.390 | 0.386 |
| .3 | 0.382 | 0.378 | 0.374 | 0.371 | 0.367 | 0.363 | 0.359 | 0.356 | 0.352 | 0.348 |
| .4 | 0.345 | 0.341 | 0.337 | 0.334 | 0.330 | 0.326 | 0.323 | 0.319 | 0.316 | 0.312 |
| .5 | 0.309 | 0.305 | 0.302 | 0.298 | 0.295 | 0.291 | 0.288 | 0.284 | 0.281 | 0.278 |
| .6 | 0.274 | 0.271 | 0.268 | 0.264 | 0.261 | 0.258 | 0.255 | 0.251 | 0.248 | 0.245 |
| .7 | 0.242 | 0.239 | 0.236 | 0.233 | 0.230 | 0.227 | 0.224 | 0.221 | 0.218 | 0.215 |
| .8 | 0.212 | 0.209 | 0.206 | 0.203 | 0.200 | 0.198 | 0.195 | 0.192 | 0.189 | 0.187 |
| .9 | 0.184 | 0.181 | 0.179 | 0.176 | 0.174 | 0.171 | 0.169 | 0.166 | 0.164 | 0.161 |
| 1.0 | 0.159 | 0.156 | 0.154 | 0.152 | 0.149 | 0.147 | 0.145 | 0.142 | 0.140 | 0.138 |
| 1.1 | 0.136 | 0.133 | 0.131 | 0.129 | 0.127 | 0.125 | 0.123 | 0.121 | 0.119 | 0.117 |
| 1.2 | 0.115 | 0.113 | 0.111 | 0.109 | 0.107 | 0.106 | 0.104 | 0.102 | 0.100 | 0.099 |
| 1.3 | 0.097 | 0.095 | 0.093 | 0.092 | 0.090 | 0.089 | 0.087 | 0.085 | 0.084 | 0.082 |
| 1.4 | 0.081 | 0.079 | 0.078 | 0.076 | 0.075 | 0.074 | 0.072 | 0.071 | 0.069 | 0.068 |
| 1.5 | 0.067 | 0.066 | 0.064 | 0.063 | 0.062 | 0.061 | 0.059 | 0.058 | 0.057 | 0.056 |
| 1.6 | 0.055 | 0.054 | 0.053 | 0.052 | 0.051 | 0.049 | 0.048 | 0.047 | 0.046 | 0.046 |
| 1.7 | 0.045 | 0.044 | 0.043 | 0.042 | 0.041 | 0.040 | 0.039 | 0.038 | 0.038 | 0.037 |
| 1.8 | 0.036 | 0.035 | 0.034 | 0.034 | 0.044 | 0.032 | 0.031 | 0.031 | 0.030 | 0.029 |
| 1.9 | 0.029 | 0.028 | 0.027 | 0.027 | 0.026 | 0.026 | 0.025 | 0.024 | 0.024 | 0.023 |
| 2.0 | 0.023 | 0.022 | 0.022 | 0.021 | 0.021 | 0.020 | 0.020 | 0.019 | 0.019 | 0.018 |
14. いろいろな確率分布2
事前に読むと理解が深まる- 学習内容が難しかった方に -
- 14. いろいろな確率分布2
14-2. 正規分布の再生性と標準正規分布
- 14. いろいろな確率分布2
14-3. 標準化したデータの使い方
- ブログ
正規分布の発見






