確率変数がポアソン分布に従っている時、の期待値と分散は次に示すように、になります。

例えば、ある街で1年間（365日）のうち雪が降る日数は平均20日のポアソン分布に従うとします。このとき、この街で1年間に雪が降る日数の期待値とその分散はともに「20」になります。

例題1：

エクセル統計開発者のKさんのもとには、1時間あたり平均5通のお問い合わせメールが届きます。1時間にお問い合わせメールが届く数がポアソン分布に従うとすると、終業時刻までの1時間の間にお問い合わせメールが1通も届かない確率はいくらでしょうか。

1時間あたりの平均お問い合わせメール数が「5」と与えられているので、となります。したがって、1時間の間にお問い合わせメールが1通も届かない確率は、

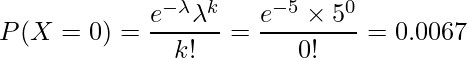
です。すなわち、お問い合わせメールが1通以上来る確率は（=99.3%）となることから、終業までの1時間の間、Kさんはのんびりできなさそうです。

例題2：

当選確率がである宝くじを200枚買う時、200枚のうち1枚だけが当たる確率はいくらでしょうか。

■ポアソン分布を用いる場合

宝くじが当たる枚数がポアソン分布に従うと仮定して解く場合、例題1とは異なり（平均当選枚数）は与えられていないことに注意しなければなりません。このようなときには、ある事象が起こる確率と試行回数からを求めます。、であることから、

となります。したがって、この宝くじが1枚だけ当選する確率は、次の式から約26.8%であると算出されます。

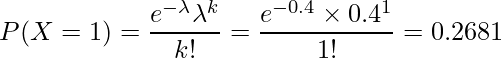
■二項分布を用いる場合

この問題は二項分布を用いて解くこともできます。二項分布の一般式に、をあてはめると約26.9%であると算出されます。この式を手で計算するのは非常に大変ですが、ポアソン分布を用いて算出された値と非常に近い値となることが分かります。

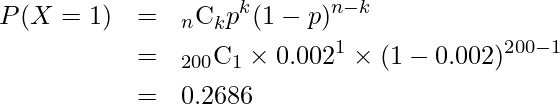
【コラム】ポアソン分布と二項分布は似ている？

ポアソン分布は二項分布から派生しており、その性質が似通っていることから例題2のようにどちらも使える場合があります。一般的に、ポアソン分布は試行回数が非常に大きく確率が非常に小さいときに使われますが、二項分布との最大の違いは「」と「」が分からなくても使えるという点です。「」すなわち「ある事象が起こる平均回数」さえ分かっていれば、例題1のようにポアソン分布から確率を算出することができます。